题目内容
解不等式|x+2|+|x-1|<4.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:通过对x≤-2、-2<x<1、x≥1的分类讨论,去掉绝对值符号,可求得对应情况下的解集,最后取其并集即可.
解答:
解:①x≤-2时,|x+2|+|x-1|<4
?-2-x+1-x<4?-2x<5?x>-
.
所以不等式组
的解集为{x|-
<x≤-2}.
②-2<x<1时,|x+2|+|x-1|<4
?x+2+1-x<4?3<4.所以不等式组
的解集为{x|-2<x<1}.
③x≥1时,|x+2|+|x-1|<4?x+2+x-1<4?2x<3?x<
.
所以不等式组
的解集为{x|1≤x<
}.
因此原不等式的解集为①②③的并集:
{x|-
<x<
}.
?-2-x+1-x<4?-2x<5?x>-
| 5 |
| 2 |
所以不等式组
|
| 5 |
| 2 |
②-2<x<1时,|x+2|+|x-1|<4
?x+2+1-x<4?3<4.所以不等式组
|
③x≥1时,|x+2|+|x-1|<4?x+2+x-1<4?2x<3?x<
| 3 |
| 2 |
所以不等式组
|
| 3 |
| 2 |
因此原不等式的解集为①②③的并集:
{x|-
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题考查绝对值不等式的解法,通过对x≤-2、-2<x<1、x≥1的分类讨论,去掉绝对值符号是关键,考查等价转化思想与运算求解能力,属于中档题

练习册系列答案
相关题目
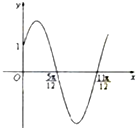 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<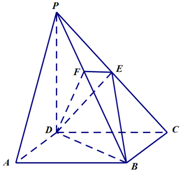 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.