题目内容
一个扇形OAB的面积是1,它的周长是4,求∠AOB的大小和弦AB的长.
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:根据题意设出扇形的弧长与半径,通过扇形的周长与面积,即可求出扇形的半径与圆心角,利用三角函数的定义求出弦AB即可.
解答:
 解析:设扇形的半径为R cm.∠AOB=α.
解析:设扇形的半径为R cm.∠AOB=α.
据题意
…(3分)
解之得
…(6分)
过O作OM⊥AB交AB于M.则AM=BM=
AB.
在Rt△AMO中,AM=sin1,∴AB=2sin1.
故∠AOB=2,弦AB的长为2sin1.…(12分)
 解析:设扇形的半径为R cm.∠AOB=α.
解析:设扇形的半径为R cm.∠AOB=α.据题意
|
解之得
|
过O作OM⊥AB交AB于M.则AM=BM=
| 1 |
| 2 |
在Rt△AMO中,AM=sin1,∴AB=2sin1.
故∠AOB=2,弦AB的长为2sin1.…(12分)
点评:本题主要考查扇形的周长与扇形的面积公式的应用,以及考查学生的计算能力,此题属于基础题型.

练习册系列答案
相关题目

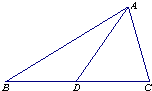 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=