题目内容
18.已知a1,$\frac{{a}_{2}}{{a}_{1}}$,$\frac{{a}_{3}}{{a}_{2}}$,…$\frac{{a}_{n}}{{a}_{n-1}}$是首项为1,公约比为2的等比数列,则数列{an}的第100顶等于24950.分析 由恒等式an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$,结合等比数列的通项公式,化简可得数列{an}的通项,即可得到所求值.
解答 解:由题意可得an=a1•$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$
=1•2•22•…•2n-1=21+2++n-1=${2}^{\frac{1}{2}n(n-1)}$,
即有数列{an}的第100顶等于${2}^{\frac{1}{2}×100×99}$=24950.
故答案为:24950.
点评 本题考查数列的通项的求法,注意运用数列的恒等式,同时考查等比数列的通项公式的运用,属于中档题.

练习册系列答案
相关题目
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
6.函数y=-cos2x+$\sqrt{3}$cosx+$\frac{5}{4}$,则( )
| A. | 最大值是$\frac{5}{4}$,最小值是1 | B. | 最大值是1,最小值是$\frac{1}{4}$-$\sqrt{3}$ | ||
| C. | 最大值是2,最小值是$\frac{1}{4}$-$\sqrt{3}$ | D. | 最大值是2,最小值是$\frac{5}{4}$ |
3.某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序对三名候选人进行了笔试和面试,成绩最高的将被推荐.各项成绩如下表所示:请你根据表中信息解答下列问题:
(1)若按笔试和面试的平均得分确定最后成绩,应当推荐谁?
(2)若笔试、面试两项得分按照6:4的比确定最后成绩,应当推荐谁?
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 85 | 95 |
| 面试 | 85 | 95 | 80 |
(2)若笔试、面试两项得分按照6:4的比确定最后成绩,应当推荐谁?
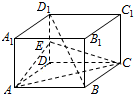 如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,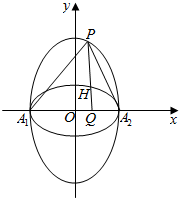 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”