题目内容
2.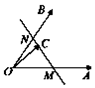 如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
分析 点C、M、N共线,可得$\overrightarrow{OC}$=$λ\overrightarrow{OM}+μ\overrightarrow{ON}$,且λ+μ=1,$\overrightarrow{OC}=\frac{1}{2}λ\overrightarrow{OM}$+$\frac{1}{2}μ\overrightarrow{OC}$,即$x+y=\frac{1}{2}(λ+μ)=\frac{1}{2}$.由$\frac{{x}^{2}+{y}^{2}}{2}≥(\frac{x+y}{2})^{2}=(\frac{1}{4})^{2}=\frac{1}{16}$.即可求解
解答 解:因为点C、M、N共线,所以$\overrightarrow{OC}$=$λ\overrightarrow{OM}+μ\overrightarrow{ON}$,且λ+μ=1,
又因为M、N分别为OA与OB的中点,∴$\overrightarrow{OC}=\frac{1}{2}λ\overrightarrow{OM}$+$\frac{1}{2}μ\overrightarrow{OC}$.,
∴$x+y=\frac{1}{2}(λ+μ)=\frac{1}{2}$.
由$\frac{{x}^{2}+{y}^{2}}{2}≥(\frac{x+y}{2})^{2}=(\frac{1}{4})^{2}=\frac{1}{16}$.
可得x2+y2$≥\frac{1}{8}$,当x=y=$\frac{1}{4}$时,取等号.
故答案为:$\frac{1}{8}$
点评 题主要考查了平面向量的应用,解题的关键是向量共线定理的应用及结论“点C、M、N共线,所以$\overrightarrow{OC}$=$λ\overrightarrow{OM}+μ\overrightarrow{ON}$,且λ+μ=1“的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 8 | B. | -8 | C. | ±8 | D. | 以上都不对 |
| A. | {x|-2≤x<1} | B. | {x|-2<x<1} | C. | {0} | D. | {0,1} |
| A. | [$\frac{1}{e}$,2e] | B. | [$\frac{1}{e}$,$\frac{2}{e}$] | C. | [$\frac{3}{e}$,2e] | D. | [$\frac{3}{e}$,$\frac{8}{{e}^{2}}$] |
| x | 1 | 2 | 3 | 4 |
| y | m | 3.2 | 4.8 | 7.5 |
 已知函数f(x)=ax3+bx2+cx有极大值5,其导函数y=f′(x)的图象经过(1,0),(2,0)点,如图所示.
已知函数f(x)=ax3+bx2+cx有极大值5,其导函数y=f′(x)的图象经过(1,0),(2,0)点,如图所示.