题目内容
11. 已知函数f(x)=ax3+bx2+cx有极大值5,其导函数y=f′(x)的图象经过(1,0),(2,0)点,如图所示.
已知函数f(x)=ax3+bx2+cx有极大值5,其导函数y=f′(x)的图象经过(1,0),(2,0)点,如图所示.(1)求原函数取得极大值时x的值(要求列表说明);
(2)求a,b,c的值.
分析 (1)观察图象满足f′(x)=0的点附近的导数的符号的变化情况,来确定极大值,求出x0的值;
(2)根据图象可得f'(1)=0,f'(2)=0,f(1)=5,建立三个方程,联立方程组求解即可.
解答 解:(1)由图象可知,
| x | (-∞,1) | 1 | (1,2) | (2,+∞) |
| f′(x) | + | 0 | - | + |
| f(x) | 递增 | 极大值 | 递减 | 递增 |
故f(x)在(-∞,1),(2,+∞)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x=1.
(2)f'(x)=3ax2+2bx+c,
由f'(1)=0,f'(2)=0,f(1)=5,
得 $\left\{\begin{array}{l}{3a+2b+c=0}\\{12a+4b+c=0}\\{a+b+c=5}\end{array}\right.$,
解得a=2,b=-9,c=12.
点评 本题主要考查了利用导数研究函数的极值,以及观察图形的能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
1.已知角α的终边经过点P(3,-4),则角α的正切值为( )
| A. | $\frac{3}{4}$ | B. | -4 | C. | $-\frac{4}{3}$ | D. | $\frac{3}{5}$ |
3.已知公差不为0的等差数列{an}满足:a1=2,且a1,a2,a5成等比数列,则数列{an}的通项公式为( )
| A. | an=2 | B. | an=n | C. | an=4n | D. | an=4n-2 |
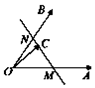 如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$. 在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10
在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10