题目内容
14.已知x与y之间的一组数据:| x | 1 | 2 | 3 | 4 |
| y | m | 3.2 | 4.8 | 7.5 |
分析 首先求得x的平均值,然后利用回归方程过样本中心点求得y的平均值,最后计算m的值即可.
解答 解:由题意可得:$\overline{x}=\frac{1+2+3+4}{4}=2.5$,
回归方程过样本中心点,则:$\overline{y}=2.1\overline{x}-1.25=2.1×2.5-1.25=4$,
即:$\frac{m+3.2+4.8+7.5}{4}=4$,解得:m=0.5.
故答案为:0.5.
点评 本题考查回归方程的性质及其应用,重点考查学生对基础概念的理解和计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知公差不为0的等差数列{an}满足:a1=2,且a1,a2,a5成等比数列,则数列{an}的通项公式为( )
| A. | an=2 | B. | an=n | C. | an=4n | D. | an=4n-2 |
4.直线xsinα+y+2=0的倾斜角的取值范围是( )
| A. | $[{\frac{π}{6},\frac{π}{4}}]$ | B. | $[{0,\frac{π}{4}}]∪[{\frac{π}{2},π}]$ | C. | $[{\frac{π}{4},\frac{3π}{4}}]$ | D. | $[{0,\frac{π}{4}}]∪[{\frac{3π}{4},π})$ |
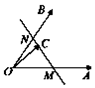 如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.