题目内容
7.若对?a∈[$\frac{1}{{e}^{2}}$,1],?b∈[-1,1],使λ+alna=2b2eb(e是自然对数的底数),则实数λ的取值范围是( )| A. | [$\frac{1}{e}$,2e] | B. | [$\frac{1}{e}$,$\frac{2}{e}$] | C. | [$\frac{3}{e}$,2e] | D. | [$\frac{3}{e}$,$\frac{8}{{e}^{2}}$] |
分析 令f(x)=xlnx,x∈[$\frac{1}{{e}^{2}}$,1],利用导数研究其单调性可得值域.令g(x)=2x2ex,x∈[-1,1],利用导数研究其单调性可得值域.根据对?a∈[$\frac{1}{{e}^{2}}$,1],?b∈[-1,1],使λ+alna=2b2eb(e是自然对数的底数),即可得出.
解答 解:令f(x)=xlnx,x∈[$\frac{1}{{e}^{2}}$,1],
f′(x)=1+lnx,令f′(x)=1+lnx=0,解得x=$\frac{1}{e}$.
∴函数f(x)在$[\frac{1}{{e}^{2}},\frac{1}{e}]$内单调递减,在$(\frac{1}{e},1]$内单调递增.
∴f(x)min=$f(\frac{1}{e})$=-$\frac{1}{e}$,
又$f(\frac{1}{{e}^{2}})$=-$\frac{2}{{e}^{2}}$,f(1)=0,∴f(x)max=f(1)=0.
∴f(x)∈$[-\frac{1}{e},0]$.
令g(x)=2x2ex,x∈[-1,1],
g′(x)=2x(x+2)ex,
∴函数g(x)在[-1,0)上单调递减,在(0,1]上单调递增.
∴g(x)min=g(0)=0.又g(-1)=$\frac{2}{e}$,g(1)=2e,∴g(x)的最大值为2e.
∴g(x)∈$[\frac{2}{e},2e]$.
∴$[λ-\frac{1}{e},λ]$=$[\frac{2}{e},2e]$.
解得λ∈$[\frac{3}{e},2e]$.
故选:C.
点评 本题考查了利用导数研究函数的单调性极值与最值、等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间X的分布列与数学期望.
| 点击量 | [0,1000] | (1000,3000] | (3000,+∞) |
| 节数 | 6 | 18 | 12 |
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间X的分布列与数学期望.
15.要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则有( )
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
12.已知函数y=f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,f(x)的导函数为f′(x)且当x>0时,xf′(x)-2f(x)<0,则一定成立的是( )
| A. | 16f(-3)>9f(4) | B. | 16f(3)<9f(-4) | C. | 9f(3)>16f(4) | D. | 9f(-3)<16f(-4) |
17.设F1,F2是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的两个焦点,点P在双曲线上,且∠F1PF2=60°,则|PF1||PF2|的值为( )
| A. | 36 | B. | 16$\sqrt{3}$ | C. | 16 | D. | 64 |
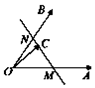 如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$.
如图所示,两个非共线向量$\overrightarrow{OA}$,$\overrightarrow{OB}$的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),则x2+y2的最小值为$\frac{1}{8}$. 在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10
在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10