题目内容
13.命题“?x0∈R,x03-x02+1>0”的否定是( )| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
分析 根据特称命题的否定是全称命题进行判断即可.
解答 解:命题是特称命题,则命题的否定是全称命题,
即?x∈R,x3-x2+1≤0,
故选:B
点评 本题主要考查含有量词的命题的否定,根据特称命题的否定是全称命题是解决本题的关键.比较基础.

练习册系列答案
相关题目
4.已知三个数a=0.32,b=log20.3,c=20.3,则a,b,c之间的大小关系是( )
| A. | b<a<c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
1.已知直线x=1上的点P到直线x-y=0的距离为$\sqrt{2}$,则点P的坐标为( )
| A. | (1,-1) | B. | (1,3) | C. | (1,-2)或(1,2) | D. | (1,-1)或(1,3) |
5.A是抛物线y2=2px(p>0)上的一点,F为抛物线的焦点,O为坐标原点,当|AF|=4时,∠OFA=120°,则抛物线的准线方程是( )
| A. | x=-1 | B. | y=-1 | C. | x=-2 | D. | y=-2 |
2.设a,b∈R,则“a+b≥4”是“a≥2且b≥2”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.要得到y=sin$\frac{x}{2}$的图象,只需将y=cos($\frac{x}{2}$-$\frac{π}{4}$)的图象上的所有点( )
| A. | 向右平移$\frac{π}{2}$ | B. | 向左平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
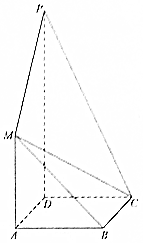 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.