题目内容
2.设a,b∈R,则“a+b≥4”是“a≥2且b≥2”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据不等式的性质结合充分条件和必要条件的定义进行判断即可.
解答 解:当a=1,b=5满足条件.a+b≥4,但a≥2且b≥2不成立,即充分性不成立,
若a≥2且b≥2,则a+b≥4成立,即必要性成立,
即“a+b≥4”是“a≥2且b≥2”的必要不充分条件,
故选:B.
点评 根据不等式的性质,利用充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
相关题目
12.已知a=sin210°,b=sin110°,c=cos180°,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
13.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
11.设函数f(x)=$\left\{\begin{array}{l}{x-2,x≥1}\\{2,x<1}\end{array}\right.$,则满足xf(x-1)≥10的x取值范围为[5,+∞).
12.“x>-2”是“(x+2)(x-3)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
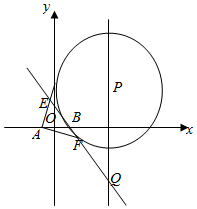 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.