题目内容
5.A是抛物线y2=2px(p>0)上的一点,F为抛物线的焦点,O为坐标原点,当|AF|=4时,∠OFA=120°,则抛物线的准线方程是( )| A. | x=-1 | B. | y=-1 | C. | x=-2 | D. | y=-2 |
分析 当|AF|=4时,∠OFA=120°,结合抛物线的定义可求得p,进而根据抛物线的性质求得抛物线的准线方程.
解答  解:由题意∠BFA=∠OFA-90°=30°,
解:由题意∠BFA=∠OFA-90°=30°,
过A作准线的垂线AC,过F作AC的垂线,垂足分别为C,B.如图,
A点到准线的距离为:d=|AB|+|BC|=p+2=4,
解得p=2,
则抛物线的准线方程是x=-1.
故选A.
点评 本题主要考查了直线与抛物线的关系,当涉及抛物线的焦点弦的问题时,常利用抛物线的定义来解决.

练习册系列答案
相关题目
15.函数f(x)=lnx+3x-7的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
13.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x03-x02+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x03-x02+1≤0 | D. | ?x∈R,x3-x2+1>0 |
20.已知集合A={1,2,3},B={x|x2-3x+a=0,a∈A},若A∩B≠∅,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |
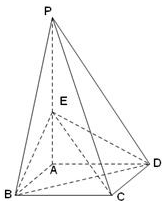 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.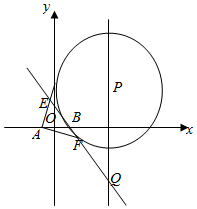 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.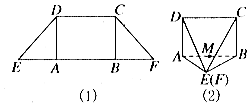 如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).
如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).