题目内容
19.(1)计算(lg2)2+lg2•lg5+lg5;(2)计算${(\root{3}{2}×\sqrt{3})^6}-8{(\frac{16}{49})^{-\frac{1}{2}}}-\root{4}{2}×{8^{0.25}}-{(-2016)^0}$.
分析 (1)利用lg2+lg5=1即可得出.
(2)利用指数幂的运算性质即可得出.
解答 解:(1)原式=lg2(lg2+lg5)+lg5=lg2+lg5=1.
(2)原式=22×33-$8×(\frac{7}{4})^{-2×(-\frac{1}{2})}$-20.25+3×0.25-1
=108-14-2-1
=91.
点评 本题考查了指数幂与对数的运算性质及其lg2+lg5=1,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
9.若全集U={1,2,3,4,5},集合M={1,2},N={2,3,4},则(∁UM)∩N等于( )
| A. | {1} | B. | {2} | C. | {3,4} | D. | {5} |
10.已知a=${∫}_{0}^{\frac{π}{2}}$(-cosx)dx,则(ax+$\frac{1}{ax}$)9展开式中,x3项的系数为( )
| A. | $\frac{63}{8}$ | B. | $\frac{63}{16}$ | C. | -84 | D. | -$\frac{63}{8}$ |
14.函数f(x)=|${log_{\frac{1}{2}}}$x|的单调递增区间是( )
| A. | $(0,\frac{1}{2}]$ | B. | (1,2] | C. | [1,+∞) | D. | (0,+∞) |
4.执行如图所示的程序框图,若输入n=5,则输出的结果是( )
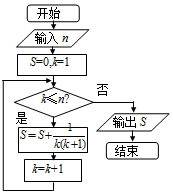

| A. | $\frac{5}{6}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{30}$ |
9.在区间[-1,3]内任取一个实数x满足log2(x-1)>0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
