题目内容
11.已知抛物线C:y2=4x,过焦点且与坐标轴不平行的直线与该抛物线相交于A、B两点,记线段AB中点为P(x0,y0).(Ⅰ)若x0=2,求直线AB的斜率;
(Ⅱ)设线段AB的垂直平分线与x轴,y轴分别相交于点D、E.当直线AB的斜率大于$\frac{{\sqrt{3}}}{3}$时,求$\frac{|AB|}{|DE|}$的取值范围.
分析 (Ⅰ)设直线方程为y=k(x-1),代入y2=4x,利用韦达定理,结合x0=2,求直线AB的斜率;
(Ⅱ)求出线段AB的垂直平分线方程,表示$\frac{|AB|}{|DE|}$,即可求$\frac{|AB|}{|DE|}$的取值范围.
解答 解:(Ⅰ)设直线方程为y=k(x-1),代入y2=4x,整理得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,∴x0=$\frac{{k}^{2}+2}{{k}^{2}}$=2,
∴k=$±\sqrt{2}$.
(Ⅱ)由(Ⅰ)知x0=$\frac{{k}^{2}+2}{{k}^{2}}$,y0=$\frac{2}{k}$,
线段AB的垂直平分线方程为y-$\frac{2}{k}$=-$\frac{1}{k}$(x-$\frac{{k}^{2}+2}{{k}^{2}}$).
令y=0,可得x=$\frac{3{k}^{2}+2}{{k}^{2}}$,令x=0,y=$\frac{3{k}^{2}+2}{{k}^{3}}$,
∴|DE|=$\frac{3{k}^{2}+2}{{k}^{3}}$•$\sqrt{{k}^{2}+1}$,
|AB|=x1+x2+p=$\frac{4({k}^{2}+1)}{{k}^{2}}$,
∴$\frac{|AB|}{|DE|}$=$\frac{4\sqrt{{k}^{2}({k}^{2}+1)}}{3{k}^{2}+2}$,
设t=3k2+2(t>3),则
$\frac{|AB|}{|DE|}$=$\frac{4}{3}\sqrt{\frac{9}{8}-2(\frac{1}{t}+\frac{1}{4})^{2}}$∈($\frac{8}{9}$,$\frac{4}{3}$).
点评 本题考查直线与抛物线的位置关系,考查抛物线的性质,考查韦达定理的运用,属于中档题.

 阅读快车系列答案
阅读快车系列答案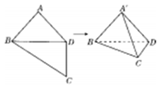 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )| A. | A'C⊥BD | B. | 四面体 A'-BCD的体积为 $\frac{1}{3}$ | ||
| C. | CA'与平面 A'BD所成的角为 30° | D. | ∠BA'C=90° |
| A. | [0,2] | B. | [-$\frac{1}{4}$,2] | C. | (0,2] | D. | (-$\frac{1}{4}$,2] |
①an=3n,②an=n2+1,③an=$\sqrt{n}$,④an=2n-n,⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有( )
| A. | ③⑤ | B. | ①②④ | C. | ③④⑤ | D. | ②③ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |