题目内容
10.已知a=${∫}_{0}^{\frac{π}{2}}$(-cosx)dx,则(ax+$\frac{1}{ax}$)9展开式中,x3项的系数为( )| A. | $\frac{63}{8}$ | B. | $\frac{63}{16}$ | C. | -84 | D. | -$\frac{63}{8}$ |
分析 利用定积分的定义求出a的值,再利用二项式展开式的通项公式求出展开式中x3项的系数.
解答 解:a═${∫}_{0}^{\frac{π}{2}}$(-cosx)dx=-sinx${|}_{0}^{\frac{π}{2}}$=-1,
则二项式(ax+$\frac{1}{ax}$)9 =(-x-$\frac{1}{x}$)9=-(x+$\frac{1}{x}$)9,
x3项的系数为开式中,通项公式为
Tr+1=-${C}_{9}^{r}$•x9-r•${(\frac{1}{x})}^{r}$=-${C}_{9}^{r}$•x9-2r,
令9-2r=3,求得 r=3,
∴展开式中x3项的系数为
x的系数为-${C}_{9}^{3}$=-84,
故选:C.
点评 本题考查了定积分的计算问题以及二项式展开式的通项公式应用问题,是基础题目.

练习册系列答案
相关题目
1.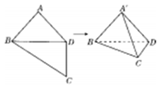 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )| A. | A'C⊥BD | B. | 四面体 A'-BCD的体积为 $\frac{1}{3}$ | ||
| C. | CA'与平面 A'BD所成的角为 30° | D. | ∠BA'C=90° |
18.已知△ABC中,a:b:c=3:2;4,则cosB=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | -$\frac{7}{8}$ |
5.在某次物理实验中,得到一组不全相等的数据x1,x2,x3,…,xn,若a是这组数据的算术平均数,则a满足( )
| A. | $\sum_{i=1}^{n}$(xi-a)最小 | B. | $\sum_{i=1}^{n}$|xi-a|最小 | ||
| C. | $\sum_{i=1}^{n}$(xi-a)2最小 | D. | $\frac{1}{n}$$\sum_{i=1}^{n}$|xi-a|最小 |
2.函数f(x)=log2$\frac{x}{2}$•log2$\frac{x}{4}$,x∈(2,8]的值域为( )
| A. | [0,2] | B. | [-$\frac{1}{4}$,2] | C. | (0,2] | D. | (-$\frac{1}{4}$,2] |