题目内容
已知△ABC的三边长是三个连续的自然数,且最大的内角是最小内角的2倍,则最小角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:余弦定理
专题:三角函数的求值
分析:设三边依次是x-1,x,x+1,其中x是自然数,且x≥2,令三角形的最小角为A,则最大角为2A,利用正弦定理列出关系式,再利用二倍角的正弦函数公式化简表示出cosA,再利用余弦定理表示出cosA,两者相等求出x的值,确定出三边长,即可求出最小值的余弦值.
解答:
解:设三边依次是x-1,x,x+1,其中x是自然数,且x≥2,
令三角形的最小角为A,则最大角为2A,
由正弦定理,有:
=
=
,
∴cosA=
,
由余弦定理,有:cosA=
,
∴
=
,即
=
=
,
整理得:(x+1)2=(x-1)(x+4),
解得:x=5,
三边长为4,5,6,
则cosA=
=
.
故选:A.
令三角形的最小角为A,则最大角为2A,
由正弦定理,有:
| x-1 |
| sinA |
| x+1 |
| sin2A |
| x+1 |
| 2sinAcosA |
∴cosA=
| x+1 |
| 2(x-1) |
由余弦定理,有:cosA=
| x2+(x+1)2-(x-1)2 |
| 2x(x+1) |
∴
| x+1 |
| 2(x-1) |
| x2+(x+1)2-(x-1)2 |
| 2x(x+1) |
| x+1 |
| x-1 |
| x2+4x |
| x2+x |
| x+4 |
| x+1 |
整理得:(x+1)2=(x-1)(x+4),
解得:x=5,
三边长为4,5,6,
则cosA=
| 52+62-42 |
| 2×5×6 |
| 3 |
| 4 |
故选:A.
点评:此题考查了正弦、余弦定理,以及二倍角的正弦函数公式,熟练掌握定理是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
某程序框图如图所示,该程序运行后输出的S的值是( )


| A、-3 | ||
B、-
| ||
C、
| ||
| D、2 |
下列四个命题中,正确的是( )
| A、“若xy=0,则x=0且y=0”的逆否命题 |
| B、“若ac2>bc2则a>b”的逆命题 |
| C、若“m>2,则不等式x2-2x+m>0的解集为R” |
| D、“正方形是菱形”的否命题 |
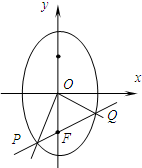 如图,已知椭圆C:
如图,已知椭圆C: