题目内容
若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中;随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位mm),将所得数据分组,得到如下频率分布表:
(Ⅰ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数;
(Ⅱ)用分层抽样的方法从差的绝对值在[-2,-1)和(3,4]的产品中抽取5个,求其中差的绝对值在[-2,-1)中的产品的个数;
(Ⅲ)在(Ⅱ)中抽取的5个产品中任取2个,差的绝对值在[-2,-1)和(3,4]中各有1个的概率.
| 分组 | 频数 | 频率 |
| [-3,-2) | 5 | 0.10 |
| [-2,-1) | 8 | 0.16 |
| (1,2] | 25 | 0.50 |
| (2,3] | 10 | 0.20 |
| (3,4] | 2 | 0.04 |
| 合计 | 50 | 1.00 |
(Ⅱ)用分层抽样的方法从差的绝对值在[-2,-1)和(3,4]的产品中抽取5个,求其中差的绝对值在[-2,-1)中的产品的个数;
(Ⅲ)在(Ⅱ)中抽取的5个产品中任取2个,差的绝对值在[-2,-1)和(3,4]中各有1个的概率.
考点:古典概型及其概率计算公式,频率分布表
专题:概率与统计
分析:(Ⅰ)依题意有
=
,解出即这批产品中的合格品的件数;
(Ⅱ)依题意知
=
,解出即所抽产品中差的绝对值在[-2,-1)中的产品的件数;
(Ⅲ)本问为古典概型的问题,需列出基本事件空间,以及事件A包含的基本事件的个数,再利用公式即可得到概率.
| 50 |
| 5000 |
| 20 |
| x+20 |
(Ⅱ)依题意知
| 8 |
| 8+2 |
| x |
| 5 |
(Ⅲ)本问为古典概型的问题,需列出基本事件空间,以及事件A包含的基本事件的个数,再利用公式即可得到概率.
解答:
解:(Ⅰ)设这批产品中的合格品数为x件,依题意有
=
,
解得x=
-20=1980,即这批产品中的合格品的件数估计是1980件;
(Ⅱ)设所抽产品中差的绝对值在[-2,-1)中的产品有x件,
依题意知
=
,解得x=4,
即所抽产品中差的绝对值在[-2,-1)中的产品有4件;
(Ⅲ)由(Ⅱ)知,所抽5件产品在[-2,-1)中有4个,在(3,4]中有1个,分别设为a1,a2,a3,a4,b,
在5个产品中任取2个的情况为:{a1,a2};{a1,a3};{a1,a4};{a1,b};
{a2,a3};{a2,a4};{a2,b};{a3,a4};{a3,b};{a4,b},共10种,
在[-2,-1)和(3,4]中各有1个的情况为{a1,b};{a2,b};{a3,b};{a4,b},共4种
故所求的概率为p=
=0.4.
| 50 |
| 5000 |
| 20 |
| x+20 |
解得x=
| 5000×20 |
| 50 |
(Ⅱ)设所抽产品中差的绝对值在[-2,-1)中的产品有x件,
依题意知
| 8 |
| 8+2 |
| x |
| 5 |
即所抽产品中差的绝对值在[-2,-1)中的产品有4件;
(Ⅲ)由(Ⅱ)知,所抽5件产品在[-2,-1)中有4个,在(3,4]中有1个,分别设为a1,a2,a3,a4,b,
在5个产品中任取2个的情况为:{a1,a2};{a1,a3};{a1,a4};{a1,b};
{a2,a3};{a2,a4};{a2,b};{a3,a4};{a3,b};{a4,b},共10种,
在[-2,-1)和(3,4]中各有1个的情况为{a1,b};{a2,b};{a3,b};{a4,b},共4种
故所求的概率为p=
| 4 |
| 10 |
点评:本题考查统计与概率知识,考查学生的计算能力和分析问题以及解决问题的能力.属于中档题.

练习册系列答案
相关题目
一算法的程序框图如右图所示,若输出的y=
,则输入的x可能为( )

| 1 |
| 2 |

| A、-1 | B、0 | C、1 | D、5 |
已知△ABC的三边长是三个连续的自然数,且最大的内角是最小内角的2倍,则最小角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
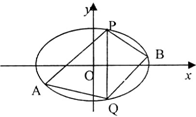 已知椭圆C的中点在原点,焦点在x轴上,离心率等于
已知椭圆C的中点在原点,焦点在x轴上,离心率等于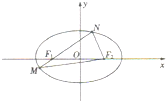 如图,椭圆E:
如图,椭圆E: 已知直线l:y=2x与抛物线C:y=
已知直线l:y=2x与抛物线C:y=