题目内容

已知函数f（x）=x2-4x+1，求函数y=f[f（x）]的值域．
考点：函数的值域
专题：配方法
分析：本题采用配方法求值域．
解答： 解：y=[f（x）]=f2（x）-4f（x）+1=[f（x）-2]2-3
=（x2-4x+1-2）2-3
=（x2-4x-1）2-3
=[（x-2）2-3]2-3≥-3，∴函数的值域为[-3，+∞）．
故答案为：[-3，+∞）．
点评：这是巧妙的运用了二次配方法求四次函数的值域，一定要注意变量的取值范围．
练习册系列答案
相关题目
对于△ABC，有如下几个结论：
①若sin2A=sin2B，则△ABC为等腰三角形；
②若Sn是等比数列{an}的前n项和，则Sn，S2n-Sn，S3n-S2n仍成等比数列．
③若sinB=cosA，则△ABC是直角三角形；
④若
a
cos
A
2
=
b
cos
B
2
=
c
cos
C
2
，则△ABC是等边三角形；
⑤P在△ABC所在平面内，且
PA
•
PB
=
PB
•
PC
=
PC
•
PA
，则点P是△ABC的垂心．
其中正确的结论序号是
 
．
已知△ABC的三边长是三个连续的自然数，且最大的内角是最小内角的2倍，则最小角的余弦值为（　　）
A、
3
4
B、
5
6
C、
7
10
D、
2
3
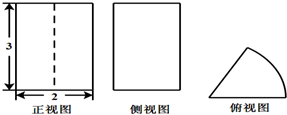某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的侧面积为（　　）
A、12+
10
3
π
B、6+
10
3
π
C、12+2π
D、6+4π
已知动圆C过定点（1，0），且与直线x=-1相切．
（Ⅰ）求动圆圆心C的轨迹方程；
（Ⅱ）设A、B是轨迹C上异于原点O的两个不同点，直线OA和OB的倾斜角分别为α和β，
 ①当α+β=
π
2
时，求证直线AB恒过一定点M；
 ②若α+β为定值θ（0＜θ＜π），直线AB是否仍恒过一定点，若存在，试求出定点的坐标；若不存在，请说明理由．
已知椭圆C两焦点坐标分别为F1(-
3
，0)，F2(
3
，0)，且经过点P(
3
，
1
2
)．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点A（0，-1），直线l与椭圆C交于两点M，N．若△AMN是以A为直角顶点的等腰直角三角形，试求直线l的方程．
设f（x）是定义在R上的奇函数，且f（x+2）=-f（x），又当-1≤x≤1时，f（x）=x3，
（1）证明：直线x=1是函数f（x）图象的一条对称轴；
（2）当x∈[1，5]时，求f（x）的解析式；
（3）求x∈R时的函数f（x）的解析式；
（4）若A={x||f（x）|＞a，x∈R}，A≠∅，求a的取值范围．
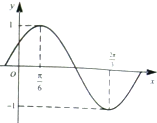已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示．
（1）求函数f（x）的解析式，并写出f（x）的单调减区间；
（2）△ABC的内角分别是A，B，C，若f（A）=1，cosB=
4
5
，求sinC的值．
已知实数x、y满足
y≤x
x+y≤2
y≥0
，那么z=x+3y的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网