题目内容
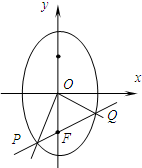 如图,已知椭圆C:x2+
如图,已知椭圆C:x2+| y2 |
| a2 |
| a2-1 |
| OP |
| OQ |
| a2(c2-m2)-1 |
| 2-c2 |
(Ⅰ)试用a表示m2;
(Ⅱ)求e的最大值;
(Ⅲ)若 e∈(
| 1 |
| 3 |
| 1 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)直线l:y=mx-c代入椭圆方程,消去x,利用韦达定理,结合向量的数量积公式,利用
•
=
,即可用a表示m2;
(Ⅱ)由c=
,m2=3-2a2,可得3(a2-c2)-2a2≥0,即可求e的最大值;
(Ⅲ)由e∈(
,
),可得
<
<
,即
<a2<
,利用m2=3-2a2,即可求m的取值范围.
| OP |
| OQ |
| a2(c2-m2)-1 |
| 2-c2 |
(Ⅱ)由c=
| a2-1 |
(Ⅲ)由e∈(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 9 |
| a2-1 |
| a2 |
| 1 |
| 4 |
| 9 |
| 8 |
| 4 |
| 3 |
解答:
 解:(Ⅰ)直线l:y=mx-c代入椭圆方程,消去x,可得(a2+m2)x2-2mcx-1=0
解:(Ⅰ)直线l:y=mx-c代入椭圆方程,消去x,可得(a2+m2)x2-2mcx-1=0
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1x2=
,
∴y1y2=(mx1-c)(mx2-c)=
,
∵
•
=
.
∴
+
=
,
∴a2+m2=2-c2=2-(a2-1),
∴m2=3-2a2;
(Ⅱ)∵c=
,m2=3-2a2,
∴3(a2-c2)-2a2≥0,
∴a2≥3c2,
∴e2≤
,
∴e的最大值
;
(Ⅲ)∵e∈(
,
),
∴e2∈(
,
),
∴
<
<
,
∴
<a2<
,
∵m2=3-2a2,
∴
<m2<
,
∴m的取值范围为(-
,-
)∪(
,
).
 解:(Ⅰ)直线l:y=mx-c代入椭圆方程,消去x,可得(a2+m2)x2-2mcx-1=0
解:(Ⅰ)直线l:y=mx-c代入椭圆方程,消去x,可得(a2+m2)x2-2mcx-1=0设P(x1,y1),Q(x2,y2),则x1+x2=
| 2mc |
| a2+m2 |
| -1 |
| a2+m2 |
∴y1y2=(mx1-c)(mx2-c)=
| a2(c2-m2) |
| a2+m2 |
∵
| OP |
| OQ |
| a2(c2-m2)-1 |
| 2-c2 |
∴
| -1 |
| a2+m2 |
| a2(c2-m2) |
| a2+m2 |
| a2(c2-m2)-1 |
| 2-c2 |
∴a2+m2=2-c2=2-(a2-1),
∴m2=3-2a2;
(Ⅱ)∵c=
| a2-1 |
∴3(a2-c2)-2a2≥0,
∴a2≥3c2,
∴e2≤
| 1 |
| 3 |
∴e的最大值
| ||
| 3 |
(Ⅲ)∵e∈(
| 1 |
| 3 |
| 1 |
| 2 |
∴e2∈(
| 1 |
| 9 |
| 1 |
| 4 |
∴
| 1 |
| 9 |
| a2-1 |
| a2 |
| 1 |
| 4 |
∴
| 9 |
| 8 |
| 4 |
| 3 |
∵m2=3-2a2,
∴
| 1 |
| 3 |
| 3 |
| 4 |
∴m的取值范围为(-
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
点评:本题考查直线与椭圆的位置关系,考查椭圆的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的三边长是三个连续的自然数,且最大的内角是最小内角的2倍,则最小角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
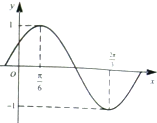 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示. 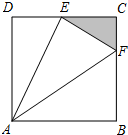 如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米).
如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米). 如图,设F(-c,0)是椭圆
如图,设F(-c,0)是椭圆