题目内容
已知二次函数f（x）=ax2+bx+c的导数f′（x），f′（0）＞0，且f（x）的值域为[0，+∞），则
的最小值为（ ）
| f(1) |
| f′(0) |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
考点：二次函数的性质
专题：函数的性质及应用
分析：由f（x）的值域为[0，+∞），可得对于任意实数x，f（x）≥0成立求出a的范围及a，b c的关系，求出f（1）及f′（0），作比后放缩去掉c，通分后利用基本不等式求最值．
解答：
解：∵f（x）的值域为[0，+∞），
即f（x）≥0恒成立，
∴
，
∴c=
．
又f′（x）=2ax+b，
∴f′（0）=b＞0，f（1）=a+b+c．
∴
=1+
=1+
=1+
≥1+
=2．
当且仅当4a2=b2时，“=”成立．
即
的最小值为2
故选：C．
即f（x）≥0恒成立，
∴
|
∴c=
| b2 |
| 4a |
又f′（x）=2ax+b，
∴f′（0）=b＞0，f（1）=a+b+c．
∴
| f(1) |
| f′(0) |
| a+c |
| b |
a+
| ||
| b |
| 4a2+b2 |
| 4ab |
2•
| ||
| 4ab |
当且仅当4a2=b2时，“=”成立．
即
| f(1) |
| f(0) |
故选：C．
点评：本题考查了函数恒成立问题，考查了导数的运算，训练了利用基本不等式求最值，关键是通过放缩转化为含有两个变量的代数式，是中档题．
练习册系列答案
相关题目
已知直线l：y=2x与抛物线C：y=如图所示程序框图中，输出S=（ ）
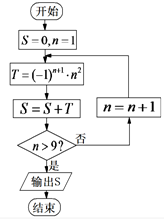
| A、45 | B、-55 |
| C、-66 | D、66 |
已知△ABC的三边长是三个连续的自然数，且最大的内角是最小内角的2倍，则最小角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法不正确的是（ ）
| A、方程f（x）=0有实数根?函数y=f（x）有零点 |
| B、函数y=-x2+3x+5有两个零点 |
| C、单调函数至多有一个零点 |
| D、函数f（x）在区间[a，b]上满足f（a）•f（b）＜0，则函数f（x）在区间（a，b）内有零点 |
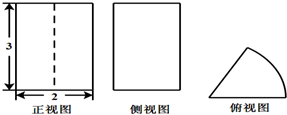某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的侧面积为（ ）A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
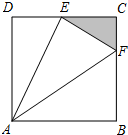如图，ABCD是边长为1百米的正方形区域，现规划建造一块景观带△ECF，其中动点E、F分别在CD、BC上，且△ECF的周长为常数a（单位：百米）．