题目内容
定义一个集合A的所有子集组成的集合叫做集合A的幂集，记为P（A），用n（A）表示有限集A的元素个数，给出下列命题：
①对于任意集合A，都有A∈P（A）；
②存在集合A，使得n[P（A）]=3；
③用∅表示空集，若A∩B=∅，则P（A）∩P（B）=∅；
④若A⊆B，则P（A）⊆P（B）；
⑤若n（A）-n（B）=1，则n[P（A）]=2×n[P（B）]．
其中正确的命题个数为（ ）
①对于任意集合A，都有A∈P（A）；
②存在集合A，使得n[P（A）]=3；
③用∅表示空集，若A∩B=∅，则P（A）∩P（B）=∅；
④若A⊆B，则P（A）⊆P（B）；
⑤若n（A）-n（B）=1，则n[P（A）]=2×n[P（B）]．
其中正确的命题个数为（ ）
| A、4 | B、3 | C、2 | D、1 |
考点：命题的真假判断与应用
专题：集合,简易逻辑
分析：直接利用新定义判断五个命题的真假即可．
解答：
解：由P（A）的定义可知①正确，④正确，
设n（A）=n，则n（P（A））=2n，∴②错误，
若A∩B=∅，则P（A）∩P（B）={∅}，③不正确；
n（A）-n（B）=1，即A中元素比B中元素多1个，
则n[P（A）]=2×n[P（B）]．⑤正确，
故选：B．
设n（A）=n，则n（P（A））=2n，∴②错误，
若A∩B=∅，则P（A）∩P（B）={∅}，③不正确；
n（A）-n（B）=1，即A中元素比B中元素多1个，
则n[P（A）]=2×n[P（B）]．⑤正确，
故选：B．
点评：本题考查集合的子集关系，集合的基本运算，新定义的理解与应用．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
设a∈R，则“a=-2”是“直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知△ABC的三边长是三个连续的自然数，且最大的内角是最小内角的2倍，则最小角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设x、y满足约束条件
，则使z=x+2y取得最大值时的最优解是（ ）
|
| A、（0，2） |
| B、（2，0） |
| C、（0，1） |
| D、（1，0） |
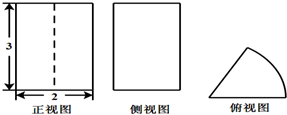某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的侧面积为（ ）A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
如图，设F（-c，0）是椭圆