题目内容
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
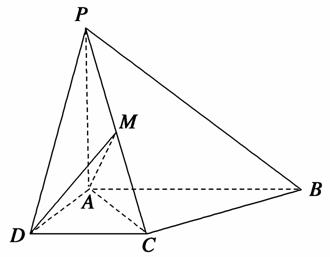
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥M-ACD的体积.
[证明] (1)由已知底面ABCD是直角梯形,AB∥DC,
又AB⊄平面PCD,CD⊂平面PCD,
∴AB∥平面PCD.
(2)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,
∴AE=DC=1
又AB=2,∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB= ,∴AD=CE=1,
,∴AD=CE=1,
则AC=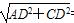 =
= ,AC2+BC2=AB2,
,AC2+BC2=AB2,
∴BC⊥AC.
又PA⊥平面ABCD,∴PA⊥BC,
又PA∩AC=A,∴BC⊥平面PAC.
(3)∵M是PC中点,
∴M到平面ADC的距离是P到平面ADC距离的一半.
∴VM-ACD=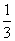 S△ACD·(
S△ACD·( PA)=
PA)=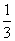 ×(
×( ×1×1)×
×1×1)× =
=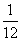 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 B.
B.
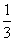 D.
D.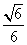
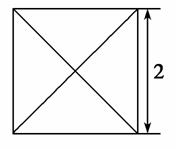
 ) D.4
) D.4
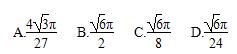
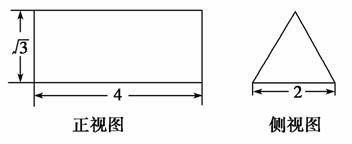
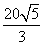 π,则这个直三棱柱的体积等于( )
π,则这个直三棱柱的体积等于( )