题目内容
8．函数f（x）=lg（3x3-$\frac{5}{2}$）的零点所在的区间是（ ）| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
分析 先确定函数的定义域和单调性，再根据f（1）＜0，f（2）＞0，得到函数的零点位于区间（1，2）．
解答 解：函数f（x）=lg（3x3-$\frac{5}{2}$）的定义域为（$\root{3}{\frac{5}{6}}$，+∞），
显然函数f（x）在定义域（$\root{3}{\frac{5}{6}}$，+∞）上单调递增，
且f（1）=lg（3-$\frac{5}{2}$）=lg$\frac{1}{2}$＜0，
而f（2）=lg（24-$\frac{5}{2}$）=lg$\frac{43}{2}$＞0，
所以，f（1）•f（2）＜0，
即f（x）的零点所在的区间为（1，2），
故答案为：A．
点评 本题主要考查了函数零点存在性定理，涉及函数定义域，单调性和函数值的计算和判断，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
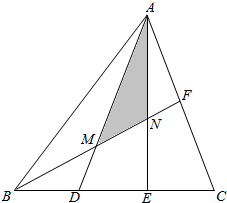△ABC中，D、E三等分BC，F为AC的中点，BF分别与AD、AE交于M、N．试求△AMN与△ABC面积之比．