题目内容

18．若函数f（x）=x2-5x+1，则f（x+1）=x2-3x-3．

分析 根据题意，由函数f（x）的解析式可得f（x+1）=（x+1）2-5（x+1）+1，变形可得答案．

解答 解：根据题意，函数f（x）=x2-5x+1，
则f（x+1）=（x+1）2-5（x+1）+1=x2-3x-3，
即f（x+1）=x2-3x-3，
故答案为：x2-3x-3．

点评 本题考查函数解析式的计算，关键要掌握函数的定义以及函数解析式的求法．

练习册系列答案
相关题目
8．函数f（x）=lg（3x3-$\frac{5}{2}$）的零点所在的区间是（　　）
A．（1，2）B．（2，3）C．（3，4）D．（4，5）
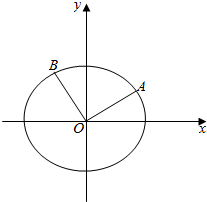9．如图，已知点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB．
（1）用α表示A，B两点的坐标；
（2）M为x轴上异于O的点，若MA⊥MB，求点M横坐标的取值范围．
6．已知△ABC的三个顶点的坐标分别为A（7，8），B（0，4），C（2，-4）．求：
（1）AB边上中线所在的直线方程；
（2）BC边上高线所在的直线方程；
（3）△ABC的面积．
13．正项数列{an}的前项和Sn，对于任意的那n∈N*，都有a13+a23+a33+…+an3=Sn2
（I）求数列{an}的通项公式an；
（Ⅱ）令bn=$\frac{{a}_{n+1}}{{{a}_{n}}^{2}•{{a}_{n+2}}^{2}}$，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有有$\frac{2}{9}$≤Tn＜$\frac{5}{16}$．
3．若函数f（x）=$\frac{2}{3}$x3-ax2+6x-3在[1，2]上单调递增，则实数a的最大值为（　　）
A．2$\sqrt{3}$B．$\sqrt{3}$C．4D．$\frac{7}{2}$
10．已知{an}是正数组成的等比数列，求证：lga1+lga3+lga5+…+lga2n-1=nlgan（n∈N*）
7．把函数f（x）=$\frac{\sqrt{2}}{2}$sin（2ωx-$\frac{π}{4}$）+$\frac{1}{2}$的图象向左平移$\frac{π}{4}$个单位，再向下平移$\frac{1}{2}$个单位后，得到函数g（x）的图象，已知g（x）的图象关于点（$\frac{π}{4}$，0）对称．
（1）求ω的值；
（2）求函数g（x）在x∈[0，4π]上的单调区间．
8．在△ABC中，角A，B，C所对应的边为a，b，c，若sin（A+$\frac{π}{6}$）=2cosA，求A的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网