题目内容
3.已知$f(x)=asin(2x+\frac{π}{6})+b$,(a,b∈R且a≠0)(1)当a=-2,b=0时,求f(x)的最小正周期与单调减区间;
(2)当$x∈[\frac{π}{4},\frac{3π}{4}]$时,其值域为[-3,1],求a,b的值.
分析 (1)当a=-2,b=0时,根据函数f(x)=-2sin(2x+$\frac{π}{6}$),求得它的周期,再根据正弦函数的单调性求得函数f(x)的减区间.
(2)由条件求得sin(2x+$\frac{π}{6}$)的范围,再分a>0、a<0两种情况,分别根据值域求得a、b的值.
解答 解:(1)当a=-2,b=0时,函数f(x)=asin(2x+$\frac{π}{6}$)+b=-2sin(2x+$\frac{π}{6}$) 的周期为$\frac{2π}{2}$=π,
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,故函数f(x)的减区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
(2)由$\frac{π}{4}≤x≤\frac{3π}{4}$,则$\frac{2π}{3}≤2x+\frac{π}{6}≤\frac{5π}{3}$,∴$-1≤sin(2x+\frac{π}{6})≤\frac{1}{2}$.
若a>0时,由$\left\{{\begin{array}{l}{-a+b=-3}\\{\frac{1}{2}a+b=1}\end{array}}\right.⇒a=\frac{8}{3}\;,b=-\frac{1}{3}$
若a<0时,由$\left\{{\begin{array}{l}{-a+b=1}\\{\frac{1}{2}a+b=-3}\end{array}}\right.⇒a=-\frac{8}{3}\;,b=-\frac{5}{3}$
综上可得:$a=\frac{8}{3}\;,b=-\frac{1}{3}或者$$a=-\frac{8}{3}\;,b=-\frac{5}{3}$.
点评 本题主要考查正弦函数的周期性、单调性、定义域和值域,属于基础题.

 名校课堂系列答案
名校课堂系列答案| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
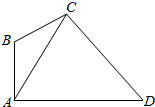 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.