题目内容
19．在平面直角坐标系xOy中，直线l：3x-y-6=0被圆C：x2+y2-2x-4y=0截得的弦长为$\sqrt{10}$．分析 求出已知圆的圆心为C（1，2），半径r=$\sqrt{5}$．利用点到直线的距离公式，算出点C到直线直线l的距离d，由垂径定理加以计算，可得直线l：3x-y-6=0被圆C：x2+y2-2x-4y=0截得的弦长．
解答 解：圆C：x2+y2-2x-4y=0，可化为（x-1）2+（y-2）2=5的圆心为C（1，2），半径r=$\sqrt{5}$，
∵点C到直线直线3x-y-6=0的距离d=$\frac{|3-2-6|}{\sqrt{9+1}}$=$\frac{5}{\sqrt{10}}$，
∴根据垂径定理，得直线l：3x-y-6=0被圆C：x2+y2-2x-4y=0截得的弦长为2$\sqrt{5-\frac{25}{10}}$=$\sqrt{10}$．
故答案为：$\sqrt{10}$．
点评 本题给出直线与圆的方程，求直线被圆截得的弦长，着重考查点到直线的距离公式、圆的方程和直线与圆的位置关系等知识，属于基础题．
练习册系列答案
相关题目
9．已知等比数列{an}为递增数列，且a52=a10，2（an+an+2）=5an+1，则数列{an}的通项公式an=（ ）
| A． | 2n | B． | 2n+1 | C． | （$\frac{1}{2}$）n | D． | （$\frac{1}{2}$）n+1 |
4．将函数$f（x）=sin（{x+\frac{π}{6}}）$的图象上各点的纵坐标不变，横坐标扩大到原来的2倍，所得函数g（x）图象的一个对称中心可以是（ ）
| A． | $（{-\frac{π}{12}，0}）$ | B． | $（{\frac{5π}{12}，0}）$ | C． | $（{-\frac{π}{3}，0}）$ | D． | $（{\frac{2π}{3}，0}）$ |
8．函数f（x）=lg（3x3-$\frac{5}{2}$）的零点所在的区间是（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
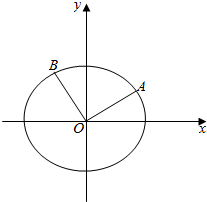如图，已知点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB．