题目内容
20.已知数列{an}是公差为d的等差数列,{bn}是公比为q(q∈R,q≠1,q≠0)的等比数列.若a1=(d-2)2,a3=d2,b1=(q-2)2,b3=q2.(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{2{b}_{2}}$+$\frac{{c}_{3}}{3{b}_{3}}$+…+$\frac{{c}_{n}}{n{b}_{n}}$=1+an+1,求数列{cn}的通项公式及前n项和Tn.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用递推关系、“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(1)∵a3-a1=2d,
∴d2-(d-2)2=2d,解得 d=2.
∴a1=0,
∴an=2(n-1).
∵$\frac{{b}_{3}}{{b}_{1}}$=q2,∴q2=$\frac{{q}^{2}}{(q-2)^{2}}$.
∵q≠0,q≠1,
∴q=3.
又b1=1,∴bn=3n-1.
(2)由题设知$\frac{{c}_{1}}{{b}_{1}}$=a2+1,∴.
当n≥2时,$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{2{b}_{2}}$+$\frac{{c}_{3}}{3{b}_{3}}$+…+$\frac{{c}_{n}}{n{b}_{n}}$=1+an+1,
$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{2{b}_{2}}$+$\frac{{c}_{3}}{3{b}_{3}}$+…+$\frac{{c}_{n-1}}{(n-1){b}_{n-1}}$=1+an,
两式相减,得$\frac{{c}_{n}}{n{b}_{n}}$=an+1-an=2.
∴cn=2nbn=2n•3n-1,(c1=3不适合).
∴cn=$\left\{\begin{array}{l}{3,n=1}\\{2n•{3}^{n-1},n≥2}\end{array}\right.$.
∴Tn=3+4×3+6×32+8×33+…+2n•3n-1,
3Tn=9+4×32+…+2(n-1)•3n-1+2n•3n,
两式相减,得
-2Tn=6+2×32+2×33+…+2×3n-1-2n•3n=$\frac{2×3({3}^{n-1}-1)}{3-1}$-2n•3n=-3+(1-2n)•3n.
∴Tn=$\frac{3}{2}$+$\frac{1}{2}(2n-1)•{3}^{n}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其求和公式、递推关系,考查了推理能力与计算能力,属于中档题.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
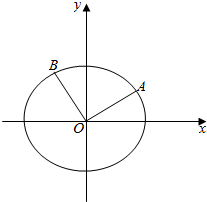 如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.
如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.