题目内容
17.已知a>0,命题p:?x>0,x+$\frac{a}{x}$≥2恒成立,命题q:?k∈R,直线kx-y+2=0与椭圆x2+$\frac{{y}^{2}}{{a}^{2}}$=1有公共点,求使得p∨q为假命题的实数a的取值范围.分析 求出命题的等价条件,结合复合命题之间的关系进行求解即可.
解答 解:命题p:因为a>0时,对?x>0,x+$\frac{a}{x}$≥2$\sqrt{a}$,则2$\sqrt{a}$≥2,即a≥1;
命题q:将直线kx-y+2=0代入椭圆x2+$\frac{{y}^{2}}{{a}^{2}}$=1得:(k2+a2)x2+4kx+4-a2=0,
则△=4a2(a2+k2-4)≥0,即a2≥-k2+4;
而-k2+4在R上的最大值为4;
∴a2≥4,∵a>0,∴解得a≥2;
(或者直线kx-y+2=0经过定点(0,2),则$0+\frac{4}{a^2}≤1$,
∵a>0,∴解得a≥2)
则p∨q为假命题时,$\left\{{\begin{array}{l}{0<a<1}\\{0<a<2}\end{array}}\right.$
综上可得,a的取值范围是0<a<1.
点评 本题主要考查复合命题的真假关系的应用,根据条件求出命题的等价条件是解决本题的关键.

练习册系列答案
相关题目
8.函数f(x)=lg(3x3-$\frac{5}{2}$)的零点所在的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
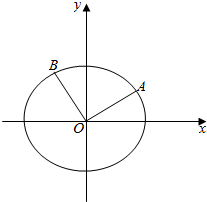 如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.
如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.