题目内容
下列命题中,是假命题的是( )
A、?x∈(0,
| ||||||||
| B、?x∈R,sin2x=2sinxcosx | ||||||||
C、|
| ||||||||
| D、4log43=3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用三角函数的单调性即可判断出正误;
B.根据倍角公式即可判断出正误;
C.由于|
•
|=|
||
||cos<
,
>|,即可判断出正误;
D.利用对数恒等式即可判断出正误.
B.根据倍角公式即可判断出正误;
C.由于|
| a |
| b |
| a |
| b |
| a |
| b |
D.利用对数恒等式即可判断出正误.
解答:
解:A.?x∈(0,
),利用三角函数的单调性可得cosx>cos(
-x)=sinx,因此正确;
B.?x∈R,根据倍角公式可得:sin2x=2sinxcosx,正确;
C.|
•
|=|
||
||cos<
,
>|,因此不正确;
D.利用对数恒等式可得:4log43=3,因此正确.
综上可得:C是假命题.
故选:C.
| π |
| 4 |
| π |
| 2 |
B.?x∈R,根据倍角公式可得:sin2x=2sinxcosx,正确;
C.|
| a |
| b |
| a |
| b |
| a |
| b |
D.利用对数恒等式可得:4log43=3,因此正确.
综上可得:C是假命题.
故选:C.
点评:本题考查了三角函数的单调性、倍角公式、数量积的定义、对数恒等式、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
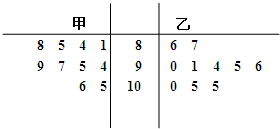 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=
不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
|
| A、(-2,0) |
| B、(-∞,0) |
| C、(0,2) |
| D、(-∞,-2) |
已知D是不等式组
所确定的平面区域,则圆x2+y2=4与D围成的区域面积为( )
|
A、
| ||
B、
| ||
| C、π | ||
D、
|
 已知在?ABCD中,点M在AB上,且AM=3MB,点N在BD上,且
已知在?ABCD中,点M在AB上,且AM=3MB,点N在BD上,且