题目内容
已知回归直线斜率的估计值为2，样本点的中心为点（4，5），则回归直线的方程为 ．
考点：线性回归方程
专题：计算题,概率与统计
分析：根据回归直线斜率的估计值为2，样本的中心点为（4，5），借助点斜式方程，可求得回归直线方程．
解答：
解：回归直线斜率的估计值为2，样本的中心点为（4，5），
根据回归直线方程恒过样本的中心点，可得回归直线方程
=2x-3．
故答案为：
=2x-3．
根据回归直线方程恒过样本的中心点，可得回归直线方程
 |
| y |
故答案为：
|
| y |
点评：本题的考点是线性回归方程，主要考查回归直线方程的求解，解题的关键是利用回归直线方程恒过样本的中心点．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
设a=log3
，b=log5
，c=log7
，则（ ）
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| A、c＞b＞a |
| B、b＞c＞a |
| C、a＞c＞b |
| D、a＞b＞c |
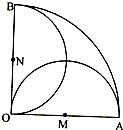如图，在圆心角为直角的扇形OAB区域中，M、N分别为OA、OB的中点，在M、N两点处各有一个通信基站，其信号的覆盖范围分别为以OA、OB为直径的圆，在扇形OAB内随机取一点，则此点无信号的概率是（ ）A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中，是假命题的是（ ）
A、?x∈（0，
| ||||||||
| B、?x∈R，sin2x=2sinxcosx | ||||||||
C、|
| ||||||||
| D、4log43=3 |
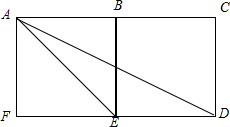如图所示，四边形ABEF和BCDE均是边长为1的正方形，在以A、B、C、D、E、F为起点和终点的向量中．函数f（x）=|log2x|+x-2的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |