题目内容
已知f(x)=
x3+ax2+(2a-1)x,f(x)在(-9,-2)上单调递减,求a的取值范围.
| 1 |
| 3 |
考点:函数的单调性与导数的关系
专题:导数的概念及应用
分析:问题等价于导函数f′(x)=x2+2ax+(2a-1)≤0在(-9,-2)上恒成立,可得只需a大于等于
在x∈(-9,-2)的最大值,由x的范围可得答案.
| 1-x |
| 2 |
解答:
解:∵f(x)=
x3+ax2+(2a-1)x,f(x)在(-9,-2)上单调递减,
∴导函数f′(x)=x2+2ax+(2a-1)≤0在(-9,-2)上恒成立,
变形可得2(x+1)a≤1-x2,∵x∈(-9,-2),∴x+1∈(-8,-1),
∴a≥
=
,只需a大于等于
在x∈(-9,-2)的最大值,
∵x∈(-9,-2),∴-x∈(2,9),∴1-x∈(3,10),
∴
∈(
,5),∴a≥5
| 1 |
| 3 |
∴导函数f′(x)=x2+2ax+(2a-1)≤0在(-9,-2)上恒成立,
变形可得2(x+1)a≤1-x2,∵x∈(-9,-2),∴x+1∈(-8,-1),
∴a≥
| 1-x2 |
| 2(1+x) |
| 1-x |
| 2 |
| 1-x |
| 2 |
∵x∈(-9,-2),∴-x∈(2,9),∴1-x∈(3,10),
∴
| 1-x |
| 2 |
| 3 |
| 2 |
点评:本题考查函数的单调性和导数的关系,涉及恒成立问题,属中档题.

练习册系列答案
相关题目
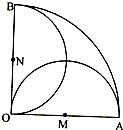 如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )
如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中,是假命题的是( )
A、?x∈(0,
| ||||||||
| B、?x∈R,sin2x=2sinxcosx | ||||||||
C、|
| ||||||||
| D、4log43=3 |
函数f(x)=|log2x|+x-2的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
 如图,将∠B=
如图,将∠B=