题目内容
已知sin(π-x)=2cosx,则sin2x+1=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系、诱导公式求得tanx=2,再根据sin2x+1=
+1=
+1,计算求得结果.
| sin2x |
| sin2x+cos2x |
| tan2x |
| tan2x+1 |
解答:
解:∵sin(π-x)=sinx=2cosx,∴tanx=2,则sin2x+1=
+1=
+1=
+1=
,
故选:D.
| sin2x |
| sin2x+cos2x |
| tan2x |
| tan2x+1 |
| 4 |
| 4+1 |
| 9 |
| 5 |
故选:D.
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是( )
| A、(-∞,-2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[1,+∞) |
下列命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| B、若p∧q为假命题,则p,q均为假命题 |
| C、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| D、对于命题p:?x∈R,x2+x+1>0,则¬p:?x∈R,x2+x+1≤0 |
已知a<b<0,c<0,则下列各式正确的是( )
| A、ac<bc | ||||
B、
| ||||
| C、(a-2)c<(b-2)c | ||||
| D、a+c<b+c |
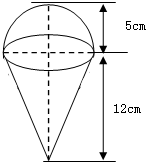 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14) 如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD.
如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD.