题目内容
4.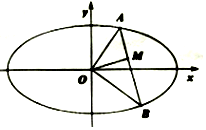 如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.
如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.(1)已知直线AB的斜率为k,用k表示线段AB的长度;
(2)过点O作OM⊥AB于M点,点P为椭圆C上一动点,求线段PM长度的取值范围.
分析 (1)由题意,可设AB:y=kx+m.与椭圆方程联立得(1+4k2)x2+8kmx+4m2-4=0,利用一元二次方程的根与系数的关系可得:|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$\frac{\sqrt{16+64{k}^{2}-16{m}^{2}}}{4{k}^{2}+1}$.又由OA⊥OB,知$-1=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{({k{x_1}+m})({k{x_2}+m})}}{{{x_1}{x_2}}}$,代入化简解出即可得出.
(2)设直线AB:y=kx+m,则$OM:y=-\frac{1}{k}x({k≠0})$,可设M(x,y),由(1)可知,5m2-4k2=4.消去m,k可得:点M的轨迹方程为${x^2}+{y^2}=\frac{4}{5}$.可得${|{PO}|_{min}}-\frac{2}{{\sqrt{5}}}≤|{PM}|≤{|{PO}|_{max}}+\frac{2}{{\sqrt{5}}}$.即可得出.
解答 解:(1)由题意,可设AB:y=kx+m.
由$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+4{y^2}-4=0}\end{array}}\right.$,得(1+4k2)x2+8kmx+4m2-4=0,
于是,${x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$(*)
则|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$\frac{\sqrt{16+64{k}^{2}-16{m}^{2}}}{4{k}^{2}+1}$.
又由OA⊥OB,知$-1=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{({k{x_1}+m})({k{x_2}+m})}}{{{x_1}{x_2}}}$,
即$({{k^2}+1}){x_1}{x_2}+km({{x_1}+{x_2}})+{m^2}=0$,将(*)代入化简得5m2-4k2=4,
所以$|{AB}|=\sqrt{1+{k^2}}\frac{{\sqrt{16+64{k^2}-16({\frac{4}{5}{k^2}+\frac{4}{5}})}}}{{4{k^2}+1}}=\frac{4}{{\sqrt{5}}}\sqrt{1+{k^2}}\frac{{\sqrt{16{k^2}+1}}}{{4{k^2}+1}}$;
(2)若设直线AB:y=kx+m,则$OM:y=-\frac{1}{k}x({k≠0})$,可设M(x,y),
由(1)可知,5m2-4k2=4(**)
由$y=-\frac{1}{k}x$,得$k=-\frac{x}{y}$,再代入y=kx+m,得$m=y+\frac{x^2}{y}$,
代入(**),有$5{({y+\frac{x^2}{y}})^2}-4\frac{x^2}{y^2}=4$,即5(y2+x2)2=4y2+4x2,
因y2+x2≠0,故有${x^2}+{y^2}=\frac{4}{5}$.
当直线AB的斜率为0或不存在时,显然符合${x^2}+{y^2}=\frac{4}{5}$.
故点M的轨迹方程为${x^2}+{y^2}=\frac{4}{5}$.
所以,${|{PO}|_{min}}-\frac{2}{{\sqrt{5}}}≤|{PM}|≤{|{PO}|_{max}}+\frac{2}{{\sqrt{5}}}$.
而|OP|的最大值为a=2,最小值为b=1,
所以,|PM|的取值范围为$1-\frac{{2\sqrt{5}}}{5}≤|{PM}|≤2+\frac{{2\sqrt{5}}}{5}$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、点的轨迹,考查了推理能力与计算能力,属于难题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | (-2,1) | B. | (-∞,1) | C. | (0,1) | D. | (-2,0] |
| A. | [0,1) | B. | (-1,+∞) | C. | (-1,1)∪[2,+∞) | D. | ∅ |
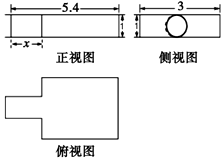 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )| A. | 0.4π+11.4立方寸 | B. | 13.8立方寸 | C. | 12.6立方寸 | D. | 16.2立方寸 |
| A. | 向左平行移动$\frac{π}{5}$个单位长度 | B. | 向右平行移动$\frac{π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{10}$个单位长度 | D. | 向右平行移动$\frac{π}{10}$个单位长度 |
| A. | y=7x+4 | B. | y=7x+2 | C. | y=x-4 | D. | y=2x-1 |
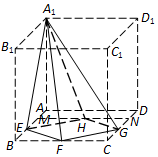 如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )
如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )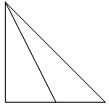
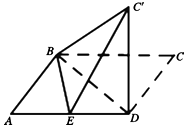 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.