题目内容
9.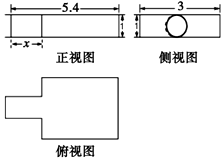 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )| A. | 0.4π+11.4立方寸 | B. | 13.8立方寸 | C. | 12.6立方寸 | D. | 16.2立方寸 |
分析 由三视图知,商鞅铜方升由一圆柱和一长方体组合而成,即可求出体积.
解答  解:由三视图知,商鞅铜方升由一圆柱和一长方体组合而成.由题意得:
解:由三视图知,商鞅铜方升由一圆柱和一长方体组合而成.由题意得:
其体积为(5.4-x)×3×1+π•($\frac{1}{2}$)2•1.6=12.6立方寸,
故选:C.
点评 本题考查的知识点是棱柱的体积和表面积,圆柱的体积和表面积,简单几何体的三视图,难度基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知a,b为实常数,{ci}(i∈N*)是公比不为1的等比数列,直线ax+by+ci=0与抛物线y2=2px(p>0)均相交,所成弦的中点为Mi(xi,yi),则下列说法错误的是( )
| A. | 数列{xi}可能是等比数列 | B. | 数列{yi}是常数列 | ||
| C. | 数列{xi}可能是等差数列 | D. | 数列{xi+yi }可能是等比数列 |
14.已知函数$f(x)=\frac{e^x}{x}+a({x-lnx})$,在$x∈({\frac{1}{2},2})$上有三个不同的极值点(e为自然对数的底数),则实数a的取值范围是( )
| A. | $({-e,-\sqrt{e}})$ | B. | $({-2\sqrt{e},-e})$ | C. | $({-\sqrt{e},0})$ | D. | $[-e,-\frac{e}{2})$ |
1.函数y=cos2x,x∈R的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 1 |
14.已知P为双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$上一点,F1、F2为双曲线的两个焦点,若∠F1PF2=60°,则△PF1F2的面积等于( )
| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 3 |
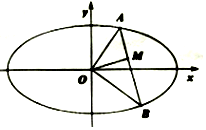 如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.
如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.