题目内容
2.设f(x)=|1-x2|,若-1<a<0,b>1且f(a)=f(b),则$\frac{b}{a-1}$的取值范围( )| A. | (-$\sqrt{2}$,-1) | B. | (-∞,-$\frac{1}{2}$) | C. | (-$\sqrt{2}$,-$\frac{1}{2}$) | D. | (-∞,-1) |
分析 根据f(a)=f(b)和a,b的范围得出a2+b2=2,即(a,b)在半径为$\sqrt{2}$的一段圆弧上,$\frac{b}{a-1}$可看做(a,b)与(1,0)连线的斜率,结合图形可得出答案.
解答  解:∵-1<a<0,b>1,f(a)=f(b),∴1-a2=b2-1,即a2+b2=2,∴(a,b)在如图所示的$\widehat{AB}$上,
解:∵-1<a<0,b>1,f(a)=f(b),∴1-a2=b2-1,即a2+b2=2,∴(a,b)在如图所示的$\widehat{AB}$上,
设M(1,0),则A(-1,1),B(0,$\sqrt{2}$),∴kAM=-$\frac{1}{2}$,kBM=-$\sqrt{2}$,
∴$-\sqrt{2}$<$\frac{b}{a-1}$<$-\frac{1}{2}$.
故选C.
点评 本题考查了分段函数的应用,线性规划,作出符合条件的区域是解题关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
7.已知点P(cosθ,sin2θ)和点Q(0,1)是两个相异点,则P、Q两点连线所在直线的倾斜角的取值范围为( )
| A. | [0,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
 一个直三棱柱被一个平面截后剩余部分的三视图如图,则截去部分的体积为$\frac{5{a}^{3}}{3}$.
一个直三棱柱被一个平面截后剩余部分的三视图如图,则截去部分的体积为$\frac{5{a}^{3}}{3}$.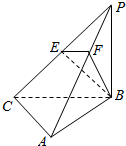 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.