题目内容
12. 一个直三棱柱被一个平面截后剩余部分的三视图如图,则截去部分的体积为$\frac{5{a}^{3}}{3}$.
一个直三棱柱被一个平面截后剩余部分的三视图如图,则截去部分的体积为$\frac{5{a}^{3}}{3}$.
分析 作出直观图,根据三视图中的数据进行计算.
解答  解:设直三棱柱为ABC-A'B'C',AB⊥BC,由三视图可知截面为四边形BCED,其中D,E为A'B'和A'C'的中点,
解:设直三棱柱为ABC-A'B'C',AB⊥BC,由三视图可知截面为四边形BCED,其中D,E为A'B'和A'C'的中点,
截去的部分为几何体BC-B'C'ED,
则截去部分的几何体体积V=V棱锥B-B′C′ED+V棱锥E-BCC′=$\frac{1}{3}×\frac{1}{2}(a+2a)a•2a$+$\frac{1}{3}×\frac{1}{2}×2a•2a•a$=$\frac{5{a}^{3}}{3}$.
故答案为$\frac{5{a}^{3}}{3}$.
点评 本题考查了空间几何体的三视图和结构特征,对于不规则几何体需分解成规则几何体进行计算.

练习册系列答案
相关题目
2.如图是一个球体和锥体的组合体的三视图,则这个组合体的体积为( )

| A. | $\frac{7}{3}$π | B. | $\frac{8}{3}$π | C. | $\frac{13}{3}$π | D. | $\frac{16}{3}$π |
20.曲线$y=\frac{-2}{x+2}+1在点(-1,-1)$处的切线方程为( )
| A. | y=2x+1 | B. | y=2x-1 | C. | y=-2x-3 | D. | y=-2x-2 |
17.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=-x2+5(x∈R) | B. | y=kx.(x∈R,k∈R,k≠0) | ||
| C. | y=x3(x∈R) | D. | $y=-\frac{1}{x}(x∈R,x≠0)$ |
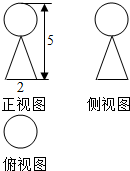
1.一个俯视图为正方形的几何体的三视图如图所示,则该几何体的体积为( )


| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
2.设f(x)=|1-x2|,若-1<a<0,b>1且f(a)=f(b),则$\frac{b}{a-1}$的取值范围( )
| A. | (-$\sqrt{2}$,-1) | B. | (-∞,-$\frac{1}{2}$) | C. | (-$\sqrt{2}$,-$\frac{1}{2}$) | D. | (-∞,-1) |
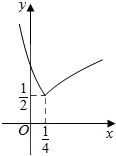 如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).
如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).