题目内容
13.(普通班)已知{an}是各项均为正数的等比数列,且a1+a2=2($\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$),a3+a4+a5=64($\frac{1}{{a}_{3}}$+$\frac{1}{{a}_{4}}$+$\frac{1}{{a}_{5}}$).(1)求{an}的通项公式;
(2)设bn=$\frac{1}{{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1)设公比为q,由已知得:$\left\{\begin{array}{l}{{a}_{1}(1+q)=\frac{2}{{a}_{1}}(1+\frac{1}{q})}\\{{a}_{1}{q}^{2}(1+q+{q}^{2})=\frac{64}{{a}_{1}{q}^{2}}(1+\frac{1}{q}+\frac{1}{{q}^{2}})}\end{array}\right.$,化简解出即可得出.
(2)bn=$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n-1}}$,再利用等比数列的前n项和公式即可得出.
解答 解:(1)设公比为q,则an=${a}_{1}{q}^{n-1}$.
由已知得:$\left\{\begin{array}{l}{{a}_{1}(1+q)=\frac{2}{{a}_{1}}(1+\frac{1}{q})}\\{{a}_{1}{q}^{2}(1+q+{q}^{2})=\frac{64}{{a}_{1}{q}^{2}}(1+\frac{1}{q}+\frac{1}{{q}^{2}})}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{{a}_{1}^{2}q=2}\\{{a}_{1}^{2}{q}^{6}=64}\end{array}\right.$,又a1>0,
解得q=2,a1=1.
∴an=2n-1.
(2)bn=$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n-1}}$,
∴数列{bn}的前n项和Tn=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=2-$\frac{2}{{2}^{n}}$.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
| 到班级宣传 | 整理、打包衣物 | 总计 | |
| 男生 | 12 | 12 | 24 |
| 女生 | 8 | 18 | 26 |
| 总计 | 20 | 30 | 50 |
(Ⅱ)用分层抽样的方法在从参与整理、打包衣物工作的志愿者中抽取5人,再从这5人中选2人.那么至少有一人是女生的概率是多少?
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| P(X2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| A. | (-$\sqrt{2}$,-1) | B. | (-∞,-$\frac{1}{2}$) | C. | (-$\sqrt{2}$,-$\frac{1}{2}$) | D. | (-∞,-1) |
| A. | (x-2)2+(y-$\frac{3}{2}$)2=$\frac{5}{4}$ | B. | (x+2)2+(y-$\frac{3}{2}$)2=$\frac{5}{4}$ | C. | (x+2)2+(y+$\frac{3}{2}$)2=$\frac{5}{4}$ | D. | (x-2)2+(y+$\frac{3}{2}$)2=$\frac{5}{4}$ |
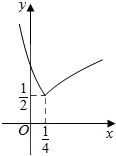 如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).
如图,函数F(x)的图象是由指数函数f(x)=bx与幂函数g(x)=xa“拼接”而成,记m=aa,n=ab,p=ba,q=bb则m,n,p,q的大小关系为p<m<q<n(用“<”连接).