题目内容
6.已知α∈[0,π],(1)若cosα=$\frac{1}{2}$,则tan2α=-$\sqrt{3}$;
(2)若sinα>cosα>$\frac{1}{2}$,则α的取值范围是($\frac{π}{4}$,$\frac{π}{3}$).
分析 (1)cosα=$\frac{1}{2}$,α∈[0,π],α=$\frac{π}{3}$,∴tan2α=tan$\frac{2π}{3}$=-$\sqrt{3}$,
(2)观察函数图象,写出α的取值范围.
解答 解:cosα=$\frac{1}{2}$,α∈[0,π],α=$\frac{π}{3}$,
∴tan2α=tan$\frac{2π}{3}$=-$\sqrt{3}$,
(2)α∈[0,π],由函数图象可知:sinα>cosα,
∴α>$\frac{π}{4}$,
cosα>$\frac{1}{2}$,
∴α<$\frac{π}{3}$,
综上可知:α的取值范围是($\frac{π}{4}$,$\frac{π}{3}$).
点评 本题考查特殊角的函数值及正弦函数余弦函数图象,属于基础题.

练习册系列答案
相关题目
16.双曲线$\frac{x^2}{m}-\frac{y^2}{4}=1$的焦点与椭圆$\frac{x^2}{20}+\frac{y^2}{4}=1$的焦点重合,则m的值等于( )
| A. | 12 | B. | 20 | C. | $2\sqrt{3}$ | D. | $2\sqrt{5}$ |
14.一底面是直角梯形的四棱柱的正(主)视图,侧(左)视图如图所示,则该四棱柱的体积为( )
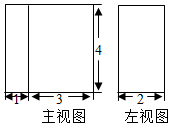

| A. | 20 | B. | 28 | C. | 20或32 | D. | 20或28 |
11.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
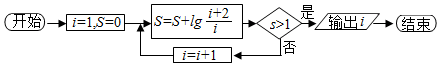
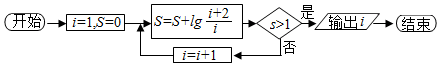
| A. | 4 | B. | 11 | C. | 13 | D. | 15 |
15.已知函数f(x)=x|x-2|,x∈R,若方程f(x)=a-|x-1|恰有5个互异的实数根,则实数a的取值范围是( )
| A. | (1,$\frac{5}{4}$) | B. | ($\frac{5}{4}$,+∞) | C. | (1,+∞) | D. | (-∞,$\frac{5}{4}$) |
16.若关于x的方程3x=$\frac{a+3}{5-a}$无负数根,则a的取值范围为( )
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
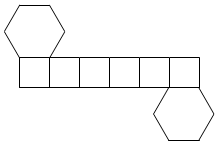 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.