题目内容
1.已知等腰三角形顶角的余弦值等于$\frac{4}{5}$,则这个三角形底角的正弦值为$\frac{3\sqrt{10}}{10}$.分析 由三角形内角和以及二倍角公式可得得cos$\frac{A}{2}$,再由诱导公式即可得解.
解答 解:设等腰三角形顶角为A,则:cosA=$\frac{4}{5}$,
由三角形的内角和可得:底角B=$\frac{π-A}{2}$=$\frac{π}{2}$-$\frac{A}{2}$,
由二倍角公式可得:cosA=2cos2$\frac{A}{2}$-1=$\frac{4}{5}$,
解方程可得:cos$\frac{A}{2}$=$\frac{3\sqrt{10}}{10}$,
由诱导公式可得:sinB=sin($\frac{π}{2}$-$\frac{A}{2}$)=cos$\frac{A}{2}$=$\frac{3\sqrt{10}}{10}$.
故答案为:$\frac{3\sqrt{10}}{10}$.
点评 本题考查三角函数恒等变换,涉及二倍角公式和三角形的内角和以及诱导公式,属基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
11.若双曲线$\frac{{x}^{2}}{3}$-$\frac{16{y}^{2}}{{p}^{2}}$=1的一个焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | 2 |
16.sin1°,sin1,sinπ°的大小顺序是( )
| A. | sin1°<sin1<sinπ° | B. | sin1°<sinπ°<sin1 | ||
| C. | sinπ°<sin1°<sin1 | D. | sin1<sin1°<sinπ° |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.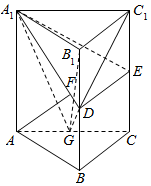 如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.