Question

15．已知函数f（x）=x|x-2|，x∈R，若方程f（x）=a-|x-1|恰有5个互异的实数根，则实数a的取值范围是（　　）

• A． （1，$\frac{5}{4}$）
• B． （$\frac{5}{4}$，+∞）
• C． （1，+∞）
• D． （-∞，$\frac{5}{4}$）

Answer 1

分析 利用参数分离法得到a=x|x-2|+|x-1|，作出函数y=x|x-2|+|x-1|的图象，利用数形结合进行求解即可．

解答 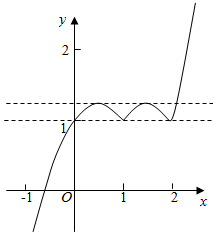：由f（x）=a-|x-1|得x|x-2|=a-|x-1|，
即a=x|x-2|+|x-1|=$\left\{\begin{array}{l}{-{x}^{2}+x+1，}&{x＜1}\\{-{x}^{2}+3x-1，}&{1≤x≤2}\\{{x}^{2}-x-1，}&{x＞2}\end{array}\right.$，
作出函数y=x|x-2|+|x-1|的图象如图，
则当x=1时，y=1，
当x=2时，y=1，
当1≤x≤2时，y=-x²+3x-1=-（x-$\frac{3}{2}$）²+$\frac{5}{4}$≤$\frac{5}{4}$，
∴要使方程f（x）=a-|x-1|恰有5个互异的实数根，
则a=x|x-2|+|x-1|有5个不同的交点，
由图象知1＜a＜$\frac{5}{4}$，
即实数a的取值范围是（1，$\frac{5}{4}$），
故选：A

点评 本题主要考查函数与方程的应用，利用参数分离法将条件转化为两个函数的图象交点问题，利用数形结合是解决本题的关键．综合性较强．