题目内容
在二项式(
+3x2)n的展开式中,各项的系数和比各项的二项式系数和大992,试求
(1)n的值.
(2)求该二项式展开式中系数最大的项.
| 3 | x2 |
(1)n的值.
(2)求该二项式展开式中系数最大的项.
考点:二项式定理的应用
专题:计算题,二项式定理
分析:(1)展开式中各项系数和为4n,二项式系数和为2n则4n-2n=992,解出即可;
(2)方法一、设系数最大项为Tr+1,则Tr-1的系数为
3r-1,Tr+1的系数为
3r,Tr+2的系数为
3r+1,列出不等式,解出整数解即可;
方法二、运用二项式定理将二项式展开,比较即得.
(2)方法一、设系数最大项为Tr+1,则Tr-1的系数为
| C | r-1 5 |
| C | r 5 |
| C | r+1 5 |
方法二、运用二项式定理将二项式展开,比较即得.
解答:
解:(1)展开式中各项系数和为4n;二项式系数和为2n
∴4n-2n=992,即(2n-32)(2n+31)=0,
解得2n=32或-31(舍去),∴n=5.
(2)设系数最大项为Tr+1,则Tr-1的系数为
3r-1
Tr+1的系数为
3r,Tr+2的系数为
3r+1,
由
3r-1≤
3r≤
3r+1,解得
≤r≤
,
又∵r∈N+,∴r=4
∴系数最大项为T5=405x
.
方法二:∵(
+3x2)5=x
+15x
+90x6+270x
+405x
+243x10
∴系数最大项为T5=405x
.
∴4n-2n=992,即(2n-32)(2n+31)=0,
解得2n=32或-31(舍去),∴n=5.
(2)设系数最大项为Tr+1,则Tr-1的系数为
| C | r-1 5 |
Tr+1的系数为
| C | r 5 |
| C | r+1 5 |
由
| C | r-1 5 |
| C | r 5 |
| C | r+1 5 |
| 7 |
| 2 |
| 9 |
| 2 |
又∵r∈N+,∴r=4
∴系数最大项为T5=405x
| 26 |
| 3 |
方法二:∵(
| 3 | x2 |
| 10 |
| 3 |
| 14 |
| 3 |
| 22 |
| 3 |
| 26 |
| 3 |
∴系数最大项为T5=405x
| 26 |
| 3 |
点评:本题考查二项式系数的性质,与各项的系数的关系,考查二项式展开式中的最大项的求法,属于中档题.

练习册系列答案
相关题目
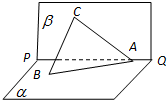 已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.
已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°. 某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:设备改造效果分析列联表
某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:设备改造效果分析列联表