题目内容
解方程：x3-13x+12=0．
考点：函数的零点
专题：函数的性质及应用
分析：把-13x拆成-x-12x进行因式分解，然后求解x的值．
解答：
解：由x3-13x+12=0，得
x3-x-12x+12=0，
即x（x2-1）-12（x-1）=0，
（x-1）（x2+x-12）=0．
解得：x=-4或x=1或x=3．
x3-x-12x+12=0，
即x（x2-1）-12（x-1）=0，
（x-1）（x2+x-12）=0．
解得：x=-4或x=1或x=3．
点评：本题考查了一元三次方程的解法，关键是正确进行因式分解，是基础题．
练习册系列答案
相关题目
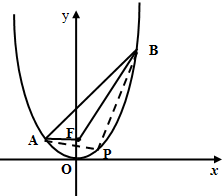如图，已知抛物线x2=4y上两定点A，B分别在对称轴左、右两侧，F为抛物线的焦点，且|AF|=2，|BF|=5．
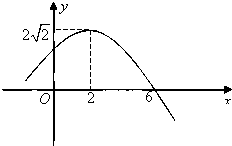已知函数y=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，|φ|＜