题目内容
(1)在z轴上求与点A(-4,1,7)和B(3,5,-2)等距离的点的坐标.
(2)在yOz平面上,求与点A(3,1,2)、B(4,-2,-2)和C(0,5,1)等距离的点的坐标.
(2)在yOz平面上,求与点A(3,1,2)、B(4,-2,-2)和C(0,5,1)等距离的点的坐标.
考点:空间两点间的距离公式,空间中的点的坐标
专题:空间位置关系与距离
分析:(1)根据C点是z轴上的点,设出C点的坐标(0,0,z),根据C点到A和B的距离相等,写出关于z的方程,解方程即可得到C的竖标,写出点C的坐标.
(2)根据点在坐标面yOz内,设出点的坐标(0,y,z),根据点到A、B、C的距离相等,写出关于y、z的方程,解方程即可得到点的坐标.
(2)根据点在坐标面yOz内,设出点的坐标(0,y,z),根据点到A、B、C的距离相等,写出关于y、z的方程,解方程即可得到点的坐标.
解答:
解:(1)由题意设C(0,0,z),
∵C与点A(-4,1,7)和点B(3,5,-2)等距离,
∴|AC|=|BC|,
∴
=
,
∴18z=28,
∴z=
,
∴C点的坐标是(0,0,
).
(2)解:设yOz平面内一点D(0,y,z)与A,B,C三点距离相等,
则有|AP|2=9+(1-y)2+(2-z)2,
|BP|2=16+(2+y)2+(2+z)2,
|CP|2=(5-y)2+(1-z)2,
由|AP|=|BP|,及|AP|=|CP|,
得
化简可得
解得
∴点P(0,1,-2)为yOz平面内到A,B,C三点等距离的点.
∵C与点A(-4,1,7)和点B(3,5,-2)等距离,
∴|AC|=|BC|,
∴
| 16+1+(7-z)2 |
| 9+25+(z+2)2 |
∴18z=28,
∴z=
| 14 |
| 9 |
∴C点的坐标是(0,0,
| 14 |
| 9 |
(2)解:设yOz平面内一点D(0,y,z)与A,B,C三点距离相等,
则有|AP|2=9+(1-y)2+(2-z)2,
|BP|2=16+(2+y)2+(2+z)2,
|CP|2=(5-y)2+(1-z)2,
由|AP|=|BP|,及|AP|=|CP|,
得
|
化简可得
|
解得
|
∴点P(0,1,-2)为yOz平面内到A,B,C三点等距离的点.
点评:本题考查两点之间的距离公式,应用两点之间的距离相等,得到方程,应用方程的思想来解题,本题是一个中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
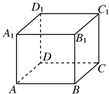 如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量
如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量| AC1 |
①(
| AB |
| BC |
| CC1 |
②(
| AA1 |
| A1D1 |
| D1C1 |
③(
| AB |
| BB1 |
| B1C1 |
④(
| AA1 |
| A1B1 |
| B1C1 |
| A、①③ | B、②④ |
| C、③④ | D、①②③④ |
函数f(x)=x-sinx是( )
| A、奇函数且单调递增 |
| B、奇函数且单调递减 |
| C、偶函数且单调递增 |
| D、偶函数且单调递减 |
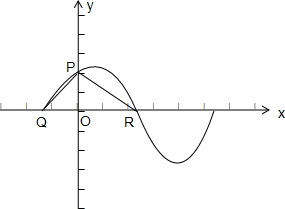 如图,点P(0,
如图,点P(0,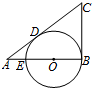 如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为
如图,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,则BC的长为