题目内容
20.圆C1:x2+y2-2x=0与圆C2:x2+(y-$\sqrt{3}$)2=4的公切线的条数( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 求出两个圆的圆心和半径,根据圆心距离和半径之间的关系,判断两个圆的位置关系即可得到结论.
解答 解:圆C1:x2+y2-2x=0的标准方程为(x-1)2+y2=1,圆心为C1:(1,0),半径r=1,
圆C2:x2+(y-$\sqrt{3}$)2=4,圆心为C2:(0,$\sqrt{3}$),半径R=2,
则|C1C2|=2,
∵R+1=3,R-1=1,
∴1<|C1C2|<3,
∴两个圆的位置关系是相交,
则两个圆的公共切线为2条,
故选B.
点评 本题主要考查圆的公共切线的条数,求出两圆的圆心和半径,判断两个圆的位置关系是解决本题的关键.

练习册系列答案
相关题目
8.等比数列{an}中,a1=3,a8=9,函数f(x)=x(x-a1)(x-a2)…(x-a8),则f'(0)=( )
| A. | 36 | B. | 39 | C. | 312 | D. | 315 |
15.已知P、Q分别在射线y=x(x>0)和y=-x(x>0)上,且△POQ的面积为1,(0为原点),则线段PQ中点M的轨迹为( )
| A. | 双曲线x2-y2=1 | B. | 双曲线x2-y2=1的右支 | ||
| C. | 半圆x2+y2=1(x<0) | D. | 一段圆弧x2+y2=1(x>$\frac{{\sqrt{2}}}{2}$) |
5.为了得到函数y=3cos2x,x∈R的图象,只需要把函数y=3cos(2x+$\frac{π}{5}$),x∈R的图象上所有的点( )
| A. | 向左平移$\frac{π}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向左平移$\frac{π}{10}$个单位长度 | D. | 向右平移$\frac{π}{10}$个单位长度 |
12.某程序框图如图所示,若运行该程序后输出的值是$\frac{9}{19}$,则整数t的值是( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
9.已知集合M={x|x2<1},N={x|x≥0},则M∩N=( )
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|-1<x≤0} |
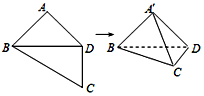 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).