题目内容
若不等式(log
x)2-6log4x+2≤0的解集为M,当x∈M时,求f(x)=a•2x+3+4x的最小值.
| 1 |
| 2 |
考点:指、对数不等式的解法
专题:不等式的解法及应用
分析:求解对数不等式得到集合M,进一步求得2x的范围,然后令t=2x换元,由对称轴的范围分类求得函数f(x)的最小值.
解答:
解:由(log
x)2-6log4x+2≤0,得
(log2x)2-3log2x+2≤0,即1≤log2x≤2,
∴2≤x≤4.
则M=[2,4],
当x∈M时,2x∈[4,16],
f(x)=a•2x+3+4x=(2x)2+8a•2x.
令t=2x∈[4,16],
则y=f(x)=t2+8at(4≤t≤16),
对称轴方程为t=-4a.
当-4a≤4,即a≥-1时,ymin=yt=4=16+32a;
当-4a≥16,即a≤-4时,ymin=yt=16=256+128a;
当4<-4a<16,即-4<a<-1时,ymin=yt=-4a=-16a2.
综上,f(x)min=
.
| 1 |
| 2 |
(log2x)2-3log2x+2≤0,即1≤log2x≤2,
∴2≤x≤4.
则M=[2,4],
当x∈M时,2x∈[4,16],
f(x)=a•2x+3+4x=(2x)2+8a•2x.
令t=2x∈[4,16],
则y=f(x)=t2+8at(4≤t≤16),
对称轴方程为t=-4a.
当-4a≤4,即a≥-1时,ymin=yt=4=16+32a;
当-4a≥16,即a≤-4时,ymin=yt=16=256+128a;
当4<-4a<16,即-4<a<-1时,ymin=yt=-4a=-16a2.
综上,f(x)min=
|
点评:本题考查了对数不等式的解法,考查了利用换元法求二次函数的最值,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数g(x)=x2-4x+9在[-2,0]上的最小值为( )
| A、5 | B、9 | C、21 | D、6 |
直线l1、l2的方向向量分别为
=(1,2,-2),
=(-2,3,2),则( )
| a |
| b |
| A、l1∥l2 |
| B、l1与l2相交,但不垂直 |
| C、l1⊥l2 |
| D、不能确定 |
“q≤1”是“函数f(x)=x2-x+q存在零点”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
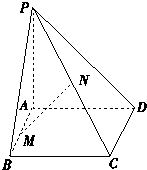 如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°,
如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°,
