题目内容
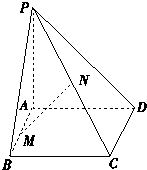 如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°,
如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°,(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用三角形的中位线得到线线平行,进一步得到线面平行,利用线线垂直进一步转化成线面垂直.
(2)利用线面垂直转化线线垂直,最后确定矩形是正方形.
(2)利用线面垂直转化线线垂直,最后确定矩形是正方形.
解答:
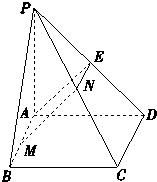 (1)证明:如图,取PD的中点E,连接AE,NE.
(1)证明:如图,取PD的中点E,连接AE,NE.
E、N分别为PD,PC的中点,
所以:EN∥CD,EN=
CD,
又M为AB的中点,
所以:AM=
CD,AM∥CD,
EN∥AM,EN=AM,
所以:四边形AMNE为平行四边形.
MN∥AE,
所以:MN∥平面PAD,
PA⊥平面ABCD,∠PDA=45°,
所以:△PAD是等腰直角三角形,
所以:AE⊥PD.
又CD⊥AD,CD⊥PA,AD交PA于A,
所以:CD⊥平面PAD,AE?平面PAD,
所以:CD⊥AE,
又CD交PD于D,
所以:AE⊥平面PCD,
则:MN⊥平面PCD,
(2)若 PC⊥BD,又PA⊥BD,PA交PC于P,
所以:BD⊥平面PAC,
所以:BD⊥AC,即矩形ABCD的对角线互相垂直.
此时矩形为正方形.
即当矩形ABCD为正方形时,满足PC⊥BD.
 (1)证明:如图,取PD的中点E,连接AE,NE.
(1)证明:如图,取PD的中点E,连接AE,NE.E、N分别为PD,PC的中点,
所以:EN∥CD,EN=
| 1 |
| 2 |
又M为AB的中点,
所以:AM=
| 1 |
| 2 |
EN∥AM,EN=AM,
所以:四边形AMNE为平行四边形.
MN∥AE,
所以:MN∥平面PAD,
PA⊥平面ABCD,∠PDA=45°,
所以:△PAD是等腰直角三角形,
所以:AE⊥PD.
又CD⊥AD,CD⊥PA,AD交PA于A,
所以:CD⊥平面PAD,AE?平面PAD,
所以:CD⊥AE,
又CD交PD于D,
所以:AE⊥平面PCD,
则:MN⊥平面PCD,
(2)若 PC⊥BD,又PA⊥BD,PA交PC于P,
所以:BD⊥平面PAC,
所以:BD⊥AC,即矩形ABCD的对角线互相垂直.
此时矩形为正方形.
即当矩形ABCD为正方形时,满足PC⊥BD.
点评:本题考查的知识要点:线面平行的判定定理,线面垂直的判定定理,属于基础题型.

练习册系列答案
相关题目
 如图,一桥拱的形状为抛物线,该抛物线拱的高为h=6m,宽为b=24m,则该抛物线拱的面积为
如图,一桥拱的形状为抛物线,该抛物线拱的高为h=6m,宽为b=24m,则该抛物线拱的面积为 如图,已知一艘船以30nmile/h的速度往北偏东10°的A岛行驶,计划到达A岛后停留10min后继续驶往B岛,B岛在A岛的北偏西60°的方向上.船到达C处时是上午10时整,此时测得B岛在北偏西30°的方向,经过20min到达D处,测得B岛在北偏西45°的方向,如果一切正常的话,此船何时能到达B岛?
如图,已知一艘船以30nmile/h的速度往北偏东10°的A岛行驶,计划到达A岛后停留10min后继续驶往B岛,B岛在A岛的北偏西60°的方向上.船到达C处时是上午10时整,此时测得B岛在北偏西30°的方向,经过20min到达D处,测得B岛在北偏西45°的方向,如果一切正常的话,此船何时能到达B岛?