题目内容
19.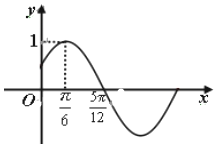 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.(Ⅰ) 求函数f(x)的解析式;
(Ⅱ) 若f($\frac{α}{2}$)=$\frac{4}{5}$,求sin($\frac{5π}{6}$-α)的值.
分析 (Ⅰ)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(Ⅱ) 若f($\frac{α}{2}$)=sin(α+$\frac{π}{6}$)=$\frac{4}{5}$,再利用诱导公式求得sin($\frac{5π}{6}$-α)的值.
解答 解:(Ⅰ)根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象,可得A=1,
∵f(x)的最小正周期为4•($\frac{5π}{12}$-$\frac{π}{6}$),故ω=2.
根据五点法作图,可得2×$\frac{π}{6}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{6}$,故函数f(x)=sin(2x+$\frac{π}{6}$).
(Ⅱ) 若f($\frac{α}{2}$)=sin(α+$\frac{π}{6}$)=$\frac{4}{5}$,则sin($\frac{5π}{6}$-α)=sin[π-(α+$\frac{π}{6}$)]=sin(α+$\frac{π}{6}$)=$\frac{4}{5}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
10.p:log2a>0是q:$\frac{1}{a}$<1 的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
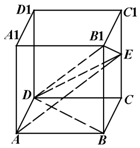 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.