题目内容
17.设复数z=$\frac{2+i}{(1+i)^{2}}$(i为虚数单位),则z的共轭复数的虚部是1.分析 直接利用复数代数形式的乘除运算化简,再求出$\overline{z}$得答案.
解答 解:由z=$\frac{2+i}{(1+i)^{2}}$=$\frac{2+i}{2i}=\frac{(2+i)(-i)}{-2{i}^{2}}=\frac{1}{2}-i$,
∴$\overline{z}=\frac{1}{2}+i$.
∴z的共轭复数的虚部是1.
故答案为:1.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
7.下面四个推理,不属于演绎推理的是( )
| A. | 因为函数y=sinx(x∈R)的值域为[-1,1],2x-1∈R,所以y=sin(2x-1)(x∈R)的值域也为[-1,1] | |
| B. | 昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿 | |
| C. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也是如此 | |
| D. | 如果一个人在墙上写字的位置与他的视线平行,那么,墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距地面六尺多,于是,他得出了凶手身高六尺多的结论 |
2.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{y≥a(x-4)}\end{array}\right.$,若z=2x+y的最小值是-1,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
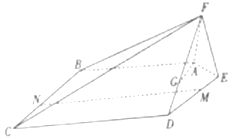 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.