题目内容
若函数f(x)=(mx-1)ex在(0,+∞)上单调递增,则实数m的取值范围是 .
考点:利用导数研究函数的单调性
专题:计算题,导数的概念及应用
分析:由f′(x)≥0可得mx+m-1≥0在(0,+∞)上恒成立,即可得出结论.
解答:
解:∵f(x)=(mx-1)ex,
∴f′(x)=(mx+m-1)ex,
由f′(x)≥0可得mx+m-1≥0在(0,+∞)上恒成立,
∴m≥
∵
<1,
∴m≥1,
故答案为:[1,+∞).
∴f′(x)=(mx+m-1)ex,
由f′(x)≥0可得mx+m-1≥0在(0,+∞)上恒成立,
∴m≥
| 1 |
| x+1 |
∵
| 1 |
| x+1 |
∴m≥1,
故答案为:[1,+∞).
点评:正确把问题等价转化、熟练掌握利用导数研究函数的单调性、极值与最值等是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知数列{an}的前n项和为Sn,且a1=1,a2=3,若对任意n∈N*,都有an+2-an=2成立,则S100=( )
| A、2550 | B、2600 |
| C、5050 | D、5100 |
定积分
cosxdx=( )
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
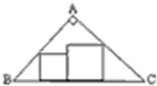 从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为
从等腰直角三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=4,∠A=90°,则这两个正方形的面积之和的最小值为