题目内容
函数f(x)=
的图象大致为( )
| 2xcos2x |
| 22x-1 |
A、 |
B、 |
C、 |
D、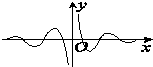 |
考点:函数的图象
专题:函数的性质及应用
分析:根据定义在R上的奇函数图象必要原点可以排除B,再利用函数的变化规律,排除B,C.问题得以解决.
解答:
解:∵f(-x)=
=-
=-f(x),
∴f(x)为奇函数,
即图象关于原点对称,故排除B,
当0<x<
0时,2x>1,22x>1,co2x>0,故f(x)>0,故排除A,
当x趋向于+∞,f(x)越来越接近x轴,故C排除,
只有D符合,
故选:D.
| 2-xcos(-2x) |
| 22(-x)-1 |
| 2xcos2x |
| 22x-1 |
∴f(x)为奇函数,
即图象关于原点对称,故排除B,
当0<x<
| π |
| 4 |
当x趋向于+∞,f(x)越来越接近x轴,故C排除,
只有D符合,
故选:D.
点评:本题考查的知识点是函数的图象,在分析非基本函数图象的形状时,特殊点、单调性、奇偶性是我们经常用的方法.

练习册系列答案
相关题目
已知
=2
,
=3
,…,
=6
,则可推测实数a,b的值分别为( )
2+
|
|
3+
|
|
6+
|
|
| A、5,24 | B、6,17 |
| C、6,35 | D、5,35 |
设不等式f(x)≥0的解集是[1,2],不等式g(x)≥0的解集为∅,则不等式
>0的解集是( )
| f(x) |
| g(x) |
| A、∅ |
| B、(-∞,1)∪(2,+∞) |
| C、[1,2] |
| D、R |
函数y=sin(-2x+
)的单调递减区间是( )
| π |
| 3 |
A、[kπ-
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[2kπ-
|
函数f(x)=
x3-4x+4的极大值与极小值之和为( )
| 1 |
| 3 |
| A、8 | ||
B、
| ||
| C、10 | ||
| D、12 |
已知直线l1:3x-
y+1=0与直线l2:
x-3y+2=0,则l1与l2的夹角为( )
| 3 |
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |