题目内容

已知
2+
2
3
=2
2
3
，
3+
3
8
=3
3
8
，…，
6+
a
b
=6
a
b
，则可推测实数a，b的值分别为（　　）
A、5，24B、6，17
C、6，35D、5，35
考点：归纳推理
专题：操作型,推理和证明
分析：根据题意，分析所给的等式，可归纳出等式
n+
n
n2-1
=n•
n
n2-1
，（n≥2且n是正整数），将n=6代入可得答案．
解答： 解：根据题意，分析所给的等式可得：
n+
n
n2-1
=n•
n
n2-1
（n≥2且n是正整数）
当n=6时，a=6，b=62-1=35；
故选：C．
点评：本题考查归纳推理，关键是根据题意所给的等式，发现其中的共同点．
练习册系列答案
相关题目
已知数列{an}中，an+1=an+2，a1=1，则前n项和为
 
．
已知数列{an}满足a1=-2，an+1=2+
2an
1-an
，则a4=
 
．
已知集合A={（x，y）|y=x}，B={（x，y）|y=x2}，则A∩B=
 
．
已知函数f（x）=
log2x，(x＞0)
3x，(x≤0)
，则f[f（
2
2
）]的值是
 
．
函数f（x）=
2xcos2x
22x-1
的图象大致为（　　）
A、
B、
C、
D、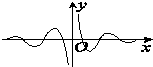
设集合A={x|x=
k
2
-
1
6
，k∈Z}，B={x|x=
k
2
+
1
3
，k∈Z}，则（　　）
A、A⊆BB、B⊆AC
C、A=BD、A∩B=∅
已知集合A={x∈Z|x（x-3）≤0}，B={x|lnx＜1}，则A∩B=（　　）
A、{0，1，2}
B、{1，2，3}
C、{1，2}
D、{2，3}
设i为虚数单位，若z=（
1+i
1-i
）2012+（
1-i
1+i
）2013，则它的共轭复数
.
z
为（　　）
A、1-iB、-1+i
C、1+iD、-1-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网