题目内容
设不等式f(x)≥0的解集是[1,2],不等式g(x)≥0的解集为∅,则不等式
>0的解集是( )
| f(x) |
| g(x) |
| A、∅ |
| B、(-∞,1)∪(2,+∞) |
| C、[1,2] |
| D、R |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:由题意可得,不等式f(x)<0的解集是{x|x<1,或x>2},不等式g(x)<0的解集为R,再把这两个集合取交集,即得不等式
>0的解集.
| f(x) |
| g(x) |
解答:
解:由于不等式f(x)≥0的解集是[1,2],不等式g(x)≥0的解集为∅,
可得不等式f(x)<0的解集是{x|x<1,或x>2},不等式g(x)<0的解集为R,
则不等式
>0的解集为{x|x<1,或x>2},
故选:B.
可得不等式f(x)<0的解集是{x|x<1,或x>2},不等式g(x)<0的解集为R,
则不等式
| f(x) |
| g(x) |
故选:B.
点评:本题主要考查其它不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知集合A={3,5,6,8},B={4,5,7,8},则A∪B的元素个数为( )
| A、6 |
| B、2 |
| C、22 |
| D、26 |
函数f(x)=
的图象大致为( )
| 2xcos2x |
| 22x-1 |
A、 |
B、 |
C、 |
D、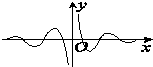 |
已知圆的半径为2,一条弦的长度等于半径,则这条弦和这条弦所对的劣弧所组成的弓形的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
点P从(1,0)出发,沿圆心在原点且半径为1的单位圆以逆时针方向运动
弧长到达Q点,则Q点的坐标为( )
| 2π |
| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
集合A={x|x-2<0},B={x|x+1<0},C={x|2x2-x-1<0},则“x∈A∩B”是“x∈C”( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在(
-
)n的二项展开式中,只有第四项的二项式系数最大,则展开式中常数项是( )
| x |
| 2 |
| 1 |
| x2 |
| A、-15 | ||
| B、15 | ||
C、-
| ||
D、
|